
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐK: x > 0
\(0< x< 1\Leftrightarrow\log_2x< 0\)
Đặt \(t=\log_2x\), pt đã cho trở thành \(t^2-2mt+m+2=0\) (1)
YCBT ↔ pt (1) có hai nghiệm âm phân biệt
\(\Leftrightarrow\begin{cases}\Delta'>0\\S< 0\\P>0\end{cases}\) \(\Leftrightarrow\begin{cases}m^2+3m+2>0\\2m< 0\\m+2>0\end{cases}\) \(\Leftrightarrow-1< m< 0\)

Chọn A.
Đặt t = x - 1 2 + 1 ≥ 1
Khi đó T = x 2 - 2 x = t 2 - 2
Khi x ∈ 0 ; 1 + 2 2 t h ì t ∈ 1 ; 3
Phương trình: m x 2 - 2 x + 2 + 1 - x 2 + 2 x = 0
trở thành m t + 1 - t 2 + 2 = 0
⇔ m = t 2 - 2 t + 1 ( * )
Đặt f t = t 2 - 2 t + 1 , t ∈ 1 ; 3
Ta có: f ' t = t 2 + 2 t + 2 t + 1 2 > 0 , ∀ t ∈ 1 ; 3
⇒ Hàm số đồng biến trên 1 ; 3
Khi đó, (*) có nghiệm t ∈ 1 ; 3
![]()
![]()
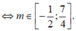
Suy ra T = 2 b - a = 4
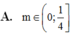
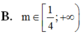
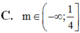


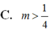



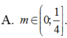
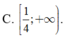
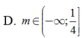
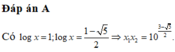
Lời giải:
Đặt \(\log_2x=t\Rightarrow x=2^t\).
Để \(x\in (0;1)\Leftrightarrow 0< 2^t< 1\Leftrightarrow t< 0\)
PT trở thành:
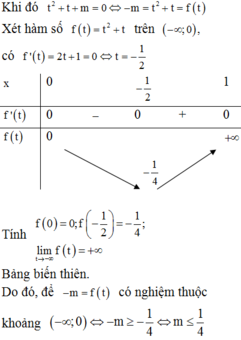
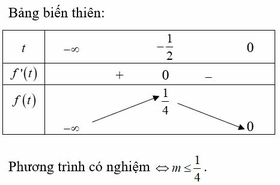
\(t^2+t+m=0\) và ta cần tìm m để pt có nghiệm âm
Điều kiện để pt có nghiệm: \(\Delta=1-4m\geq 0\Leftrightarrow m\leq \frac{1}{4}\) (1)
Áp dụng hệ thức Viete, để PT có nghiệm âm thì:
\(\left\{\begin{matrix} t_1+t_2< 0\\ t_1t_2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -1< 0\\ m> 0\end{matrix}\right.\Leftrightarrow m> 0\) (2)
Từ (1)(2) suy ra \(0< m\leq \frac{1}{4}\)
thks bạn.