Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ĐKXĐ: x\(\in\)R\{3}
b: ĐKXĐ: \(\left\{{}\begin{matrix}x>1\\x\ne2\end{matrix}\right.\)

a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)

1.
Đặt \(x^2-2x+m=t\), phương trình trở thành \(t^2-2t+m=x\)
Ta có hệ \(\left\{{}\begin{matrix}x^2-2x+m=t\\t^2-2t+m=x\end{matrix}\right.\)
\(\Rightarrow\left(x-t\right)\left(x+t-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=t\\x=1-t\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=x^2-2x+m\\x=1-x^2+2x-m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-x^2+3x\\m=-x^2+x+1\end{matrix}\right.\)
Phương trình hoành độ giao điểm của \(y=-x^2+x+1\) và \(y=-x^2+3x\):
\(-x^2+x+1=-x^2+3x\)
\(\Leftrightarrow x=\dfrac{1}{2}\Rightarrow y=\dfrac{5}{4}\)
Đồ thị hàm số \(y=-x^2+3x\) và \(y=-x^2+x+1\):
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi \(m< \dfrac{5}{4}\)
Mà \(m\in\left[-10;10\right]\Rightarrow m\in[-10;\dfrac{5}{4})\)
Có cách nào lm bài này bằng cách lập bảng biến thiên k ạ

\(\Leftrightarrow\left[{}\begin{matrix}4x-2m-\dfrac{1}{2}>-x^2+2x+\dfrac{1}{2}-m\\4x-2m-\dfrac{1}{2}< x^2-2x-\dfrac{1}{2}+m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+2x-\dfrac{1}{4}-m>0\\x^2-6x+3m>0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}1+\dfrac{1}{4}+m< 0\\9-3m< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m< -\dfrac{5}{4}\\m>3\end{matrix}\right.\)
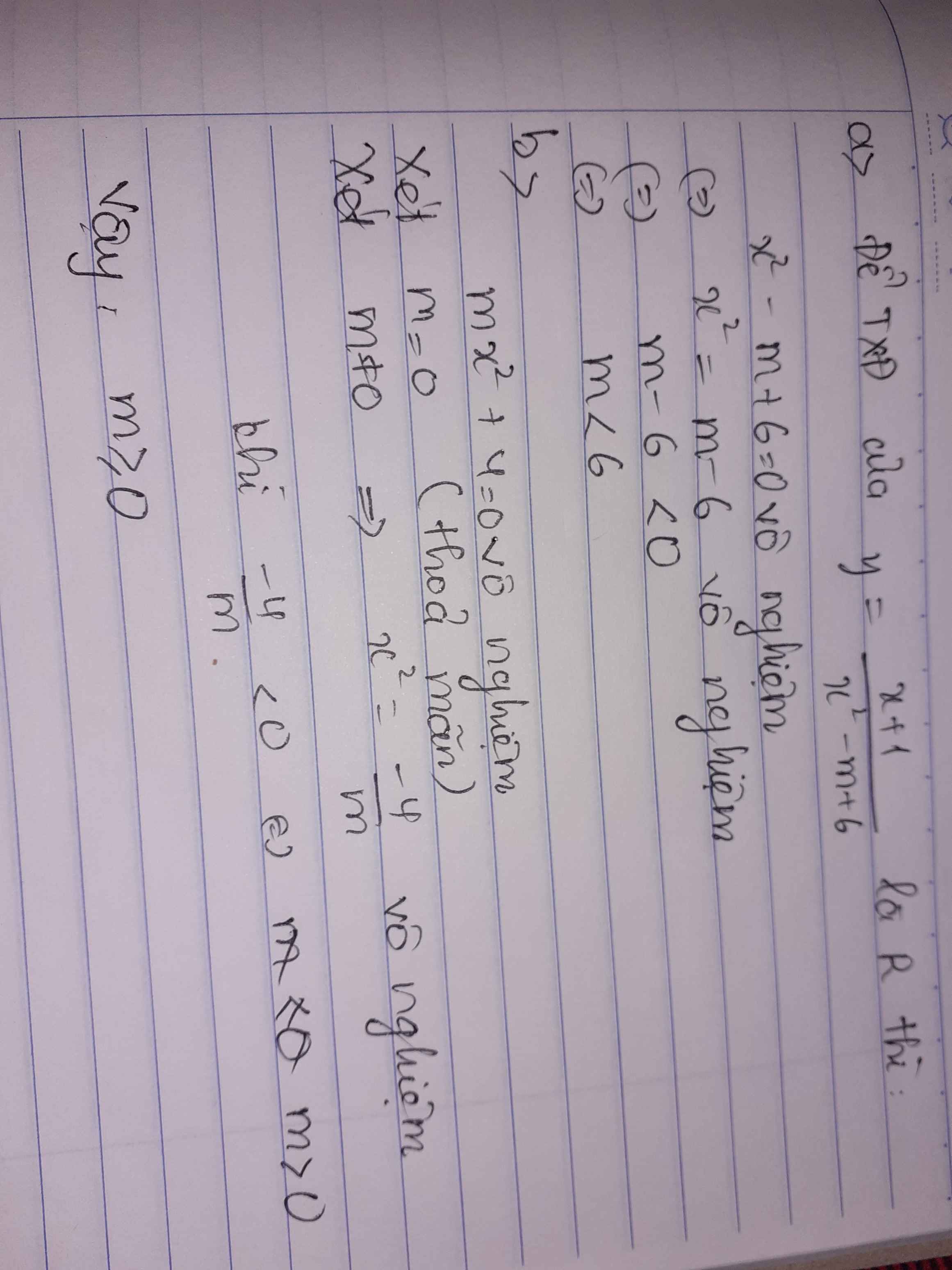
Sửa đề: TXĐ là R
a: Để hàm số sau có TXĐ là R thì 2x^2-x+m-2>0 với mọi x
=>\(\left\{{}\begin{matrix}\left(-1\right)^2-4\cdot2\left(m-2\right)< 0\\2>0\end{matrix}\right.\Leftrightarrow1-8m+16< 0\)
=>-8m+17<0
=>-8m<-17
=>m>17/8
b: Để hàm số có TXĐ là R thì x^2-4x-m+1>0 với mọi x
=>\(\left\{{}\begin{matrix}1>0\\\left(-4\right)^2-4\left(-m+1\right)< 0\end{matrix}\right.\Leftrightarrow16+4m-4< 0\)
=>4m+12<0
=>m<-3