
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`A=2x^2-2xy-6x+y^2+10`
`A=x^2-2xy+y^2+x^2-6x+10`
`A=(x-y)^2+x^2-6x+9+1`
`A=(x-y)^2+(x-3)^2+1`
Vì `(x-y)^2+(x-3)^2>=0=>A>=1`
Dấu "=" xảy ra khi `{(x-y=0),(x-3=0):}<=>x=y=3`

A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2

Xét biểu thức \(A=x\left(x-3\right)\left(x-4\right)\left(x-7\right)=\left(x^2-7x\right)\left(x^2-7x+12\right)\)
Đặt \(x^2-7x+6\rightarrow t\)Khi đó \(A=\left(t-6\right)\left(t+6\right)=t^2-36\ge-36\)
Dấu "=" xảy ra khi và chỉ khi \(t=0\)hay \(x^2-7x+6=0=>\left(x-6\right)\left(x-1\right)=0=>\orbr{\begin{cases}x=6\\x=1\end{cases}}\)
Vậy GTNN của biểu thức \(A=-36\)đạt được khi \(x=6orx=1\)
Xét biểu thức \(B=2x^2+y^2-2xy-2x+3=\left(x^2-2xy+y^2\right)+x^2-2x+1+2\)
\(=\left(x-y\right)^2+\left(x-1\right)^2+2\ge2\)
Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x-y=0\\x-1=0\end{cases}< =>\hept{\begin{cases}1-y=0\\x=1\end{cases}}< =>\hept{\begin{cases}x=1\\y=1\end{cases}< =>x=y=1}}\)
Vậy GTNN của biểu thức \(B=2\)đạt được khi \(x=y=1\)

\(A=\left(x^2-6x+9\right)+2=\left(x-3\right)^2+2\ge2\\ A_{min}=2\Leftrightarrow x=3\\ B=2\left(x^2-10x+25\right)+51=2\left(x-5\right)^2+51\ge51\\ B_{min}=51\Leftrightarrow x=5\\ C=\left[\left(x^2-4xy+4y^2\right)+10\left(x-2y\right)+25\right]+\left(y^2-2y+1\right)+2\\ C=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\\ C_{min}=2\Leftrightarrow\left\{{}\begin{matrix}x-2y+5=0\\y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y-5=2-5=-3\\y=1\end{matrix}\right.\)
a) \(A=\left(x^2-6x+9\right)+2=\left(x-3\right)^2+2\ge2\)
\(minA=2\Leftrightarrow x=3\)
b) \(B=2\left(x^2-10x+25\right)+51=2\left(x-5\right)^2+51\ge51\)
\(minB=51\Leftrightarrow x=5\)
c) \(C=\left[x^2-2x\left(2y-5\right)+\left(2y-5\right)^2\right]+\left(y^2-2y+1\right)+2=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\)
\(minC=2\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)

A= 2x^2 + y^2 - 2xy -2x+3
A= x^2-2xy + y^2 + x^2 - 2x+ 1 +2
A= (x-y)^2 + (x-1)^2 + 2
(x-y)^2> hoặc = 0 với mọi giá trị của x
(x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 + 2 > hoặc =2
=> A lớn hơn hoặc bằng 2
=> GTNN của A=2 tại x=y=1

\(1,\\ a,A=4x^2\left(-3x^2+1\right)+6x^2\left(2x^2-1\right)+x^2\\ A=-12x^4+4x^2+12x^2-6x^2+x^2=-x^2=-\left(-1\right)^2=-1\\ b,B=x^2\left(-2y^3-2y^2+1\right)-2y^2\left(x^2y+x^2\right)\\ B=-2x^2y^3-2x^2y^2+x^2-2x^2y^3-2x^2y^2\\ B=-4x^2y^3-4x^2y^2+x^2\\ B=-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^3-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^2+\left(0,5\right)^2\\ B=\dfrac{1}{8}-\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{8}\)
\(2,\\ a,\Leftrightarrow10x-16-12x+15=12x-16+11\\ \Leftrightarrow-14x=-4\\ \Leftrightarrow x=\dfrac{2}{7}\\ b,\Leftrightarrow12x^2-4x^3+3x^3-12x^2=8\\ \Leftrightarrow-x^3=8=-2^3\\ \Leftrightarrow x=2\\ c,\Leftrightarrow4x^2\left(4x-2\right)-x^3+8x^2=15\\ \Leftrightarrow16x^3-8x^2-x^3+8x^2=15\\ \Leftrightarrow15x^3=15\\ \Leftrightarrow x^3=1\Leftrightarrow x=1\)

a: \(\dfrac{2x^4-x^3-x^2+7x-4}{x^2+x-1}\)
\(=\dfrac{2x^4+2x^3-2x^2-3x^3-3x^2+3x+4x^2+4x-4}{x^2+x-1}\)
=2x^2-3x+4
b: \(=\dfrac{y}{x\left(2x-y\right)}+\dfrac{4x}{y\left(y-2x\right)}\)
\(=\dfrac{y^2-4x^2}{xy\left(2x-y\right)}=\dfrac{-\left(2x-y\right)\left(2x+y\right)}{xy\left(2x-y\right)}=\dfrac{-2x-y}{xy}\)
c: \(=\dfrac{6\left(x+8\right)}{7\left(x-1\right)}\cdot\dfrac{\left(x-1\right)^2}{\left(x-8\right)\left(x+8\right)}=\dfrac{6\left(x-1\right)}{7\left(x-8\right)}\)
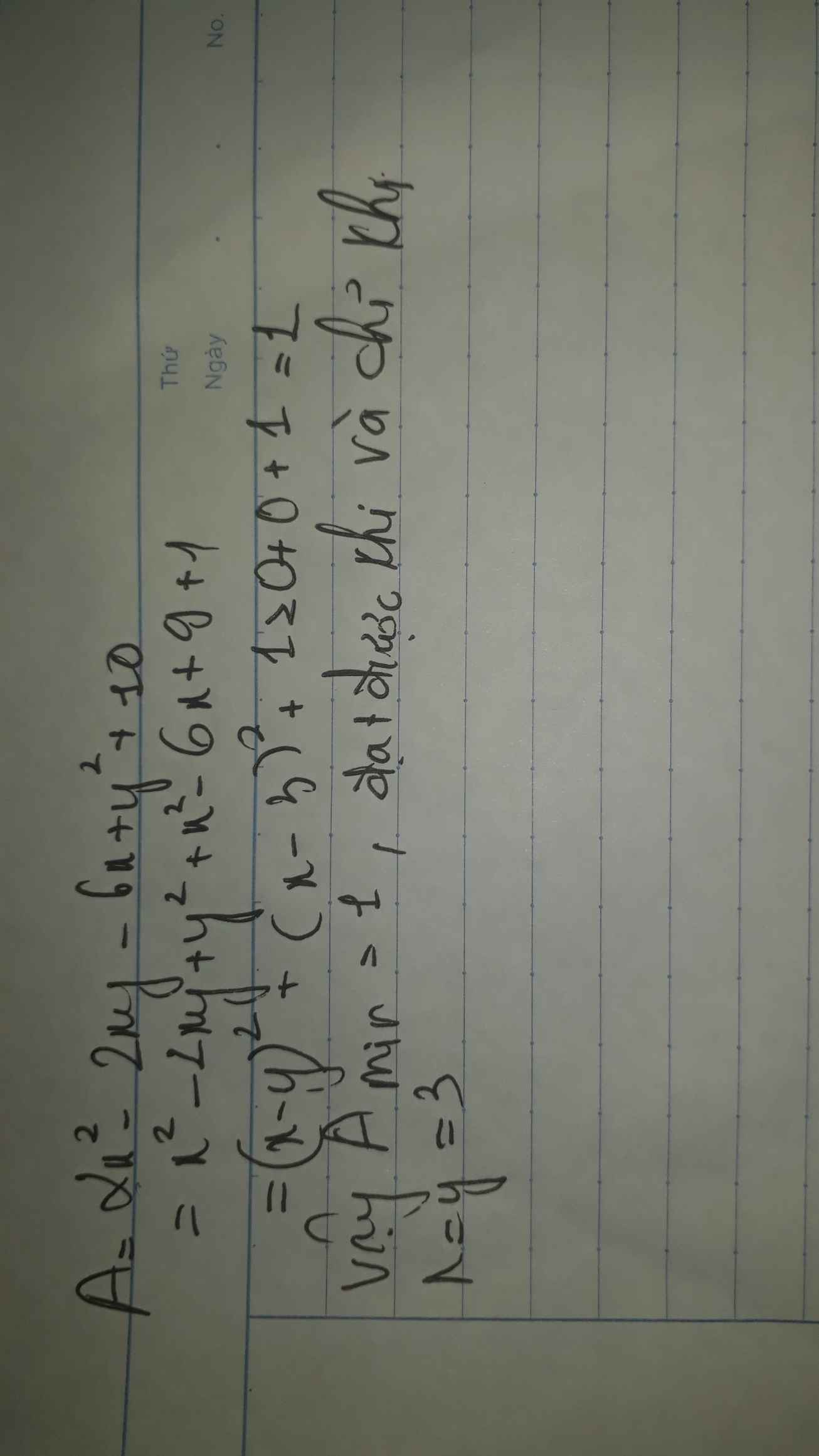
a) \(A=x^2+6x+10\)
\(A=x^2+2\cdot x\cdot3+3^2+1\)
\(A=\left(x+3\right)^2+1\ge1\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow x+3=0\Leftrightarrow x=-3\)
b) \(B=2x^2+y^2+2xy+4x+15\)
\(B=\left(x^2+2xy+y^2\right)+\left(x^2+2\cdot x\cdot2+2^2\right)+11\)
\(B=\left(x+y\right)^2+\left(x+2\right)^2+11\ge11\forall x;y\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x+y=0\\x+2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}y=2\\x=-2\end{cases}}\)