NM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
3
1 tháng 7 2018
Ta có :
\(C=4x^2+y^2+4x-6y+14\)
\(C=\left(4x^2+4x+1\right)+\left(y^2-6x+9\right)+4\)
\(C=\left(2x+1\right)^2+\left(y-3\right)^2+4\ge4\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(\hept{\begin{cases}\left(2x+1\right)^2=0\\\left(y-3\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}2x+1=0\\y-3=0\end{cases}}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}2x=-1\\y=3\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{-1}{2}\\y=3\end{cases}}}\)
Vậy GTNN của \(C\) là \(4\) khi \(x=\frac{-1}{2}\) và \(y=3\)
Chúc bạn học tốt ~
1 tháng 7 2018
\(C=4x^2+y^2+4x-6y+14\)
\(C=\left(4x^2+4x+1\right)+\left(y^2-6y+9\right)+4\)
\(C=\left(2x+1\right)^2+\left(y-3\right)^2+4\)
Mà \(\left(2x+1\right)^2\ge0\forall x\)
\(\left(y-3\right)^2\ge0\forall y\)
\(\Rightarrow C\ge4\)
Dấu "=" xảy ra khi :
\(\hept{\begin{cases}2x+1=0\\y-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-\frac{1}{2}\\y=3\end{cases}}\)
Vậy \(C_{Min}=4\Leftrightarrow\left(x;y\right)=\left(-\frac{1}{2};3\right)\)
28 tháng 7 2018
A = (2m-5)^2 -(2m+5)^2 +40m
= 4m^2 -20m+25 -(4m^2 +20m+25) + 40m
= 4m^2 -20m+25 -4m^2 -20m -25 + 40m
= 0.
Vậy biểu thức A ko phụ thuộc vào biến.
Bài 2:
Gọi 2 số nguyên liên tiếp là a và a+1 (a thuộc Z)
Ta có: (a+1)^2 -a^2
= a^2 +2a +1- a^2
= 2a+1
Mà 2a+1 là số lẻ nên (a+1)^2 -a^2 là số lẻ.
Vậy hiệu các bình phương của 2 số nguyên liên tiếp là số lẻ.
Bài 3:
P = (3x+4)^2 -10x- (x-4)(x+4)
= 9x^2 +24x +16 -10x - (x^2 -16)
= 9x^2 +24x +16 -10x -x^2 +16
= 8x^2 +14x +32
Bài 4:
Ta có: x^2 -4x+5
= (x^2 -4x+4)+ 1
= (x-2)^2 + 1
Vì (x-2)^2 >=0 với mọi x nên (x-2)^2 + 1 >=1 với mọi x.
Do đó: P = x^2 -4x+5 >=1 với mọi x.
Dấu "=" xảy ra khi: (x-2)^2 = 0
x-2 = 0
x = 2
Vậy GTNN của P là 1 tại x = 2.
Chúc bạn học tốt.
T
1
31 tháng 10 2021
\(E=22x-23-5x+2-3x+1\)
\(=14x-20\)
\(=14\cdot\dfrac{-2}{3}-20=\dfrac{-28}{3}-\dfrac{60}{3}=-\dfrac{88}{3}\)
LB
1
5 tháng 8 2019
\(\left(8-5x\right)\left(x+2\right)+4\left(x-2\right)\left(x+1\right)=\left(x-2\right)\left(x+2\right)\)
\(\Rightarrow8x+16-5x^2-10x+4x^2+4x-8x-8=x^2-4\)
\(\Rightarrow-6x-x^2-8-x^2+4=0\)
\(\Rightarrow-6x-2x^2-4=0\)
\(\Rightarrow-2\left(3x+x^2+2\right)=0\)
\(\Rightarrow\left(x+1,5\right)^2-0,25=0\)
\(\Rightarrow\left(x+2\right)\left(x+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x+2=0\\x+1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=-2\\x=-1\end{cases}}}\)
21 tháng 7 2018
B1 Xét (7x+1)\(^2\)-(x+7)\(^2\)-48(x\(^2\)-1)
=49\(x^2\)+14x+1-x\(^2\)-14x-49-48x\(^2\)+48
=0
Vậy \(\left(7x+1\right)^2-\left(x+7\right)^2=48\left(x^2-1\right)\)
B2 \(16x^2-\left(4x-5\right)^2=15\)
(4x)\(^2\)-(4x-5)\(^2\)-15=0
(4x-4x+5)(4x+4x-5)-15=09x-5)=0
5(8x-5)-15=0
40x-25-15=0
40x-40=0
x =1
câu B3 mình không bik làm
chúc bạn học tốt ~~~
5 tháng 4 2019
\(P=\frac{2x-1}{x^2-2}\left(ĐKXĐ:x\ne\pm\sqrt{2}\right)\)
\(\Leftrightarrow Px^2-2P=2x-1\)
\(\Leftrightarrow Px^2-2x-2P+1=0\)
*Nếu P = 0 thì ....
*Nếu P khác 0 thì pt trên là bậc 2
\(\Delta'=1-P\left(2P+1\right)=-2P^2-P+1\)
Có nghiệm thì \(\Delta'\ge0\Leftrightarrow-1\le P\le\frac{1}{2}\)
Nên Pmin = -1
Đến đây dạng này khi biết kết quả thì phân tích dễ r ha , từ làm nốt câu còn lại nhé , tương tự luôn
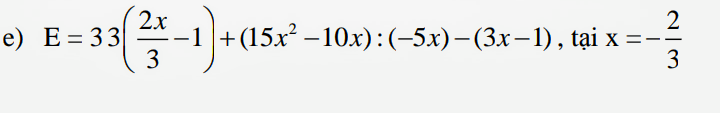
Ta có : B = \(3x^2+x+5\)
\(=2x^2+x^2+x+\frac{1}{4}+\frac{19}{4}\)
\(=2x^2+\left(x+\frac{1}{2}\right)^2+\frac{19}{4}\)
Vì \(2x^2\ge0\forall x\)
\(\left(x+\frac{1}{2}\right)^2\ge0\forall x\)
Nên : \(B=2x^2+\left(x+\frac{1}{2}\right)^2+\frac{19}{4}\ge0+0+\frac{19}{4}=\frac{19}{4}\)
Vậy \(B_{min}=\frac{19}{4}\) hơ icos vấn đề