NM
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
NV
1
10 tháng 8 2016
C=-|x+4|+2005
Ta thấy: \(\left|x+4\right|\ge0\)
\(\Rightarrow-\left|x+4\right|\le0\)
\(\Rightarrow-\left|x+4\right|+2005\le0+2005=2005\)
\(\Rightarrow C\le2005\)
Dấu = khi -|x+4|=0 <=> x=-4
Vậy MaxC=2005 khi x=-4
DT
0
15 tháng 1 2021
Bài 1:
A = 3(x + 1)2 + 5
Ta có: (x + 1)2 \(\ge\) 0 Với mọi x
\(\Rightarrow\) 3(x + 1)2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 3(x + 1)2 + 5 \(\ge\) 5 với mọi x
Hay A \(\ge\) 5
Dấu "=" xảy ra khi và chỉ khi x + 1 = 5 hay x = -1
Vậy...
B = 2|x + y| + 3x2 - 10
Ta có: 2|x + y| \(\ge\) 0 với mọi x, y
3x2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 2|x + y| + 3x2 - 10 \(\ge\) -10 với mọi x,y
Dấu "=" xảy ra khi và chỉ khi x + y = 0; x = 0
\(\Rightarrow\) x = y = 0
Vậy ...
C = 12(x - y)2 + x2 - 6
Ta có: 12(x - y)2 \(\ge\) 0 với mọi x; y
x2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 12(x - y)2 + x2 - 6 \(\ge\) -6 với mọi x, y
Dấu "=" xảy ra khi và chỉ khi x = y = 0
Phần D ko rõ đầu bài nha vì D luôn có một giá trị duy nhất
Bài 2:
Phần A ko rõ đầu bài!
B = 3 - (x + 1)2 - 3(x + 2y)2
Ta có: -(x + 1)2 \(\le\) 0 với mọi x
-3(x + 2y)2 \(\le\) 0 với mọi x, y
\(\Rightarrow\) 3 - (x + 1)2 - 3(x + 2y)2 \(\le\) 3 với mọi x, y
Dấu "=" xảy ra khi và chỉ khi x = 2y; x + 1 = 0
\(\Rightarrow\) x = -1; y = \(\dfrac{-1}{2}\)
Vậy ...
C = -12 - 3|x + 1| - 2(y - 1)2
Ta có: -3|x + 1| \(\le\) 0 với mọi x
-2(y - 1)2 \(\le\) 0 với mọi y
\(\Rightarrow\) -12 - 3|x + 1| - 2(y - 1)2 \(\le\) -12 với mọi x, y
Dấu "=" xảy ra khi và chỉ khi x + 1 = 0; y - 1 = 0
\(\Rightarrow\) x = -1; y = 1
Vậy ...
Phần D đề ko rõ là \(\dfrac{5}{2x^2}-3\) hay \(\dfrac{5}{2}\)x2 - 3 nữa
F = \(\dfrac{-5}{3}\) - 2x2
Ta có: -2x2 \(\le\) 0 với mọi x
\(\Rightarrow\) \(\dfrac{-5}{3}-2x^2\) \(\le\) \(\dfrac{-5}{3}\) với mọi x
Dấu "=" xảy ra khi và chỉ khi x = 0
Vậy ...
Chúc bn học tốt!
H
0
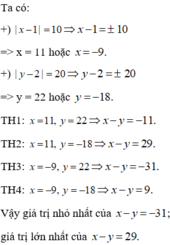
b) Ta có :
\(\left(x-8\right)^2\ge0;\forall x\)
\(\Rightarrow\left(x-8\right)^2+2019\ge2019;\forall x\)
Hay\(B\ge2019;\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x-8\right)^2=0\)
\(\Leftrightarrow x=8\)
Vậy MIN B=2019 \(\Leftrightarrow x=8\)
c) Vì \(\hept{\begin{cases}-|20-x|\le0;\forall x\\-|70+y|\le0;\forall y\end{cases}}\)
\(\Rightarrow-|20-x|-|70+y|\le0;\forall x,y\)
\(\Rightarrow90-|20-x|-|70+y|\le90-0;\forall x,y\)
Hay \(C\le90;\forall x,y\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}|20-x|=0\\|70+y|=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=20\\y=-70\end{cases}}\)
Vậy MAX C=90 \(\Leftrightarrow\hept{\begin{cases}x=20\\y=-70\end{cases}}\)