Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(A=2x^2-2xy-y^2+2xy=2x^2-y^2\)
\(=2\cdot\dfrac{4}{9}-\dfrac{1}{9}=\dfrac{7}{9}\)
b: \(B=5x^2-20xy-4y^2+20xy=5x^2-4y^2\)
\(=5\cdot\dfrac{1}{25}-4\cdot\dfrac{1}{4}\)
=1/5-1=-4/5
c \(C=x^3+6x^2+12x+8=\left(x+2\right)^3=\left(-9\right)^3=-729\)
d: \(D=20x^3-10x^2+5x-20x^2+10x+4\)
\(=20x^3-30x^2+15x+4\)
\(=20\cdot5^3-30\cdot5^2+15\cdot2+4=1784\)

Câu 1 :
\(\left(2x+y\right)\left(4x^2-2xy+y^2\right)=\left(2x\right)^3+y^3=8x^3+y^3\)Câu 2:
\(A=3\left(2x-3\right)\left(3x+2\right)-2\left(x+4\right)\left(4x-3\right)+9x\left(4-x\right)=0\)\(\Leftrightarrow3\left(6x^2-2x-6\right)-2\left(4x^2+13x-12\right)+36x-9x^2=0\)\(\Leftrightarrow18x^2-6x-18-8x^2-26x+24+36x-9x^2=0\)\(\Leftrightarrow x^2+4x+6=0\)
\(\Leftrightarrow\left(x+2\right)^2=-2\)
Ta có:
\(\left(x+2\right)^2\ge0\forall x\)
Vậy pt vô nghiệm
Vậy:ko......
Câu 3:
\(\left(5x-3\right)\left(7x+2\right)-35x\left(x-1\right)=42\)
\(\Leftrightarrow35x^2+10x-21x-6-35x^2+35x-42=0\)\(\Leftrightarrow14x=48\Leftrightarrow x=\dfrac{7}{24}\)
Câu 4:
\(\left(3x+5\right)\left(2x-1\right)+\left(5-6x\right)\left(x+2\right)=x\)
\(\Leftrightarrow6x^2-3x+10x-5+5x+10-6x^2-12x-x=0\)\(\Leftrightarrow-x=-5\Rightarrow x=5\)
câu 6,
Câu 6: \(\left(10x+9\right)x-\left(5x-1\right)\left(2x+3\right)=8\)
\(\Rightarrow10x^2+9x-\left(10x^2-2x+15x-3\right)=8\)
\(\Rightarrow10x^2+9x-10x^2+2x-15x+3=8\)
\(\Rightarrow-4x+3=8\)
\(\Rightarrow-4x=5\Rightarrow x=\dfrac{-5}{4}\)
Câu 7: \(x\left(x+1\right)\left(x+6\right)-x^3=5x\)
\(\Rightarrow\left(x^2+x\right)\left(x+6\right)-x^3=5x\)
\(\Rightarrow x^3+x^2+6x^2+6x-x^3=5x\)
\(\Rightarrow7x^2=-x\)
\(\Rightarrow7x=-1\Rightarrow x=\dfrac{-1}{7}\).

mk gợi ý, phần còn lại tự làm
a) \(A=x^2+2x+5=\left(x+1\right)^2+4\ge4\)
b) \(B=4x^2+4x+11=\left(2x+1\right)^2+10\ge10\)
c) \(\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\)
d) \(D=x^2-2x+y^2-4y+7=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\)
e) \(E=x^2-4xy+5y^2+10x-22y+28=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\)
a) A = x2 + 2x + 5
= x2 + 2x + 1 + 4
= ( x + 1 )2 + 4
Nhận xét :
( x + 1 )2 > 0 với mọi x
=> ( x + 1 )2 + 4 > 4
=> A > 4
=> A min = 4
Dấu " = " xảy ra khi : ( x + 1 )2 = 0
=> x + 1 = 0
=> x = - 1
Vậy A min = 4 khi x = - 1
b) B = 4x2 + 4x + 11
= ( 2x )2 + 4x + 1 + 10
= ( 2x + 1 )2 + 10
Nhận xét :
( 2x + 1 )2 > 0 với mọi x
=> ( 2x + 1 )2 + 10 > 10
=> B > 10
=> B min = 10
Dấu " = " xảy ra khi : ( 2x + 1 )2 = 0
=> 2x + 1 = 0
=> x = \(\frac{-1}{2}\)
Vậy Bmin = 10 khi x = \(\frac{-1}{2}\)
c) C = ( x - 1 ) ( x + 2 ) ( x + 3 ) ( x + 6 )
= [ ( x - 1 ) ( x + 6 ) ] [ ( x + 2 ) ( x + 3 ) ]
= ( x2 + 5x - 6 ) ( x2 + 5x + 6 )
= ( x2 + 5x ) 2 - 62
= ( x2 + 5x )2 - 36
Nhận xét :
( x2 + 5x )2 > 0 với mọi x
=> ( x2 + 5x )2 - 36 > - 36
=> C > - 36
=> C min = - 36
Dấu " = " xảy ra khi : ( x2 + 5x )2 = 0
=> x2 + 5x = 0
=> x ( x + 5 ) = 0
=> \(\orbr{\begin{cases}x=0\\x+5=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=0\\x=-5\end{cases}}\)
Vậy C min = - 36 khi x = 0 hoặc x = - 5
d) D = x2 - 2x + y2 - 4y + 7
= ( x2 - 2x + 1 ) + ( y2 - 4x + 4 ) + 2
= ( x - 1 )2 + ( y - 2 )2 + 2
Nhận xét :
( x - 1 )2 > 0 với mọi x
( y - 2 )2 > 0 với mọi y
=> ( x - 1 )2 + ( y - 2 )2 > 0
=> ( x - 1 )2 + ( y - 2 )2 + 2 > 2
=> D > 2
=> D min = 2
Dấu " = " xảy ra khi : \(\hept{\begin{cases}\left(x-1\right)^2=0\\\left(y-2\right)^2=0\end{cases}}\)
=> \(\hept{\begin{cases}x-1=0\\y-2=0\end{cases}}\)
=> \(\hept{\begin{cases}x=1\\y=2\end{cases}}\)
Vậy D min = 2 khi x = 1 và y = 2

Bài 1:
a) \(3x^2-2x(5+1,5x)+10=3x^2-(10x+3x^2)+10\)
\(=10-10x=10(1-x)\)
b) \(7x(4y-x)+4y(y-7x)-2(2y^2-3,5x)\)
\(=28xy-7x^2+(4y^2-28xy)-(4y^2-7x)\)
\(=-7x^2+7x=7x(1-x)\)
c)
\(\left\{2x-3(x-1)-5[x-4(3-2x)+10]\right\}.(-2x)\)
\(\left\{2x-(3x-3)-5[x-(12-8x)+10]\right\}(-2x)\)
\(=\left\{3-x-5[9x-2]\right\}(-2x)\)
\(=\left\{3-x-45x+10\right\}(-2x)=(13-46x)(-2x)=2x(46x-13)\)
Bài 2:
a) \(3(2x-1)-5(x-3)+6(3x-4)=24\)
\(\Leftrightarrow (6x-3)-(5x-15)+(18x-24)=24\)
\(\Leftrightarrow 19x-12=24\Rightarrow 19x=36\Rightarrow x=\frac{36}{19}\)
b)
\(\Leftrightarrow 2x^2+3(x^2-1)-5x(x+1)=0\)
\(\Leftrightarrow 2x^2+3x^2-3-5x^2-5x=0\)
\(\Leftrightarrow -5x-3=0\Rightarrow x=-\frac{3}{5}\)
\(2x^2+3(x^2-1)=5x(x+1)\)

1,
a,\(2x\left(3x^2-5x+3\right)\)
\(=6x^3-10x^2+6x\)
b,\(-2x\left(x^2+5x-3\right)\)
\(=-2x^3-10x^2+6x\)
c,\(-\dfrac{1}{2}x\left(2x^3-4x+3\right)\)
\(=-x^4+2x^2-\dfrac{3}{2}x\)
Bài 2:
a) \(\left(2x-1\right)\left(x^2-5-4\right)\)
\(=\left(2x-1\right)\left(x^2-9\right)\)
\(=2x^3-18x-x^2+9\)
b) \(-\left(5x-4\right)\left(2x+3\right)\)
\(=-\left(10x^2+15x-8x-12\right)\)
\(=-10x^2-7x+12\)
c) \(\left(2x-y\right)\left(4x^2-2xy+y^2\right)\)
\(=8x^3-y^3\)

\(A=x^2-4x-x\left(x-4\right)-15\)
\(=x^2-4x-x^2+4x-15=-15\) => đpcm
\(B=5x\left(x^2-x\right)-x^2\left(5x-5\right)-13\)
\(=5x^3-5x^2-5x^3+5x^2-13=-13\) => đpcm
\(C=-3x\left(x-5\right)+3\left(x^2-4x\right)-3x+7\)
\(=-3x^2+15x+3x^2-12x-3x+7=7\) => đpcm
\(D=7\left(x^2-5x+3\right)-x\left(7x-35\right)-14\)
\(=7x^2-35x+21-7x^2+35x-14=7\) => đpcm
\(E=4x\left(x^2-7+2\right)-4\left(x^3-7x+2x-5\right)\)
\(=4x^3-20x-4x^3+20x+20=20\) => đpcm
\(H=x\left(5x-3\right)-x^2\left(x-1\right)+x\left(x^2-6x\right)-10+3x\)
\(=5x^2-3x-x^3+x^2+x^3-6x^2-10x+3x=-10\) => đpcm

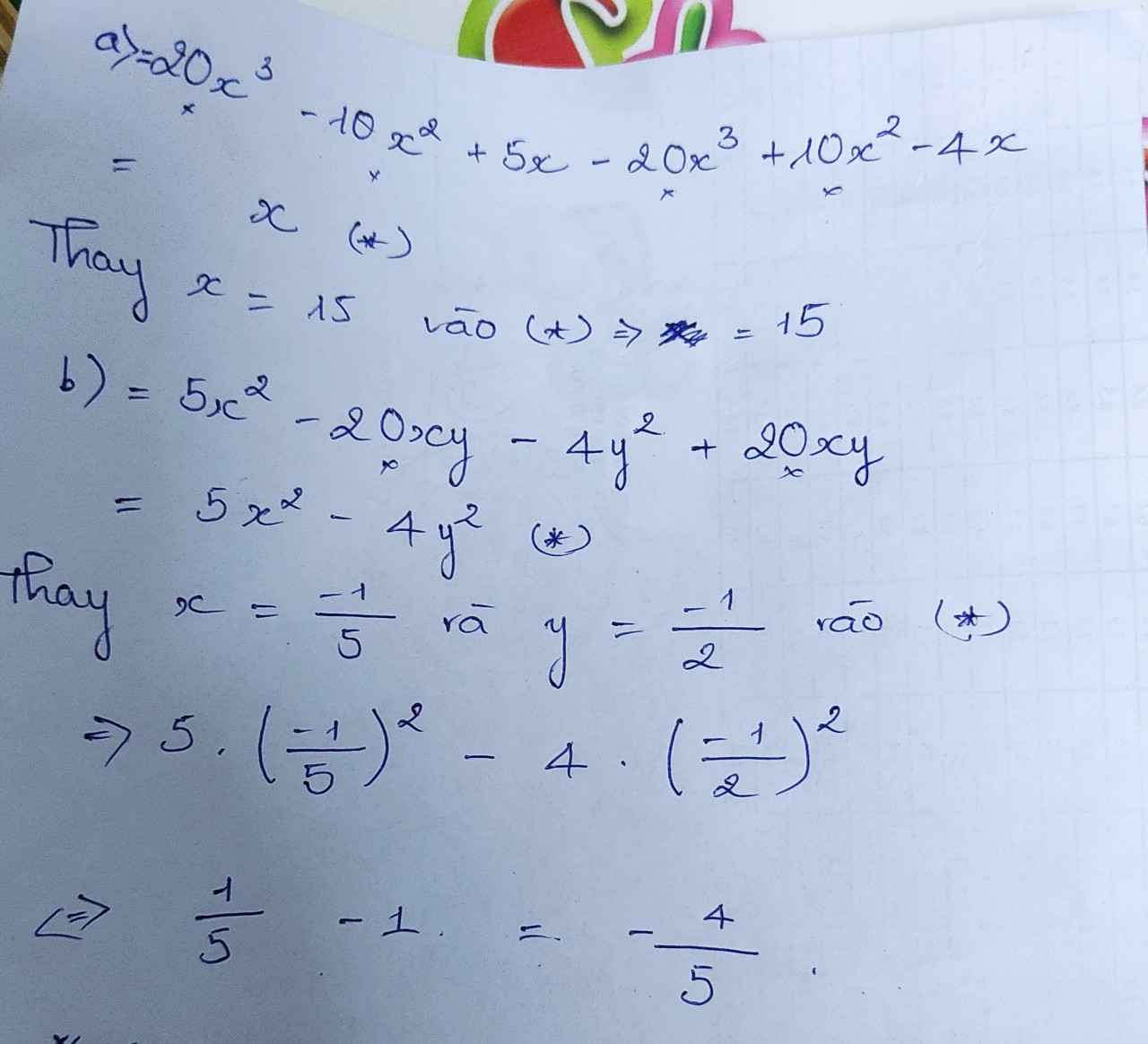
\(A=3x^2-5x+3=3(x^2-\frac{5}{3}x)+3\)
\(=3(x^2-\frac{5}{3}x+\frac{5^2}{6^2})+\frac{11}{12}=3(x-\frac{5}{6})^2+\frac{11}{12}\)
Vì \((x-\frac{5}{6})^2\geq 0, \forall x\Rightarrow A\geq 3.0+\frac{11}{12}=\frac{11}{12}\)
Vậy A(min)$=\frac{11}{12}$ khi $x=\frac{5}{6}$
\(B=2x^2+2x+1=2(x^2+x+\frac{1}{4})+\frac{1}{2}\)
\(=2(x+\frac{1}{2})^2+\frac{1}{2}\geq 2.0+\frac{1}{2}=\frac{1}{2}\)
Vậy \(B_{\min}=\frac{1}{2}\) tại \((x+\frac{1}{2})^2=0\Leftrightarrow x=\frac{-1}{2}\)
C)
\(C=2x^2+y^2+10x-2xy+27\)
\(=(x^2+10x+25)+(x^2+y^2-2xy)+2\)
\(=(x+5)^2+(x-y)^2+2\)
Vì \((x+5)^2\ge 0, (x-y)^2\geq 0\Rightarrow C\geq 0+0+2=2\)
Vậy \(C_{\min}=2\) tại \(\left\{\begin{matrix} (x+5)^2=0\\ (x-y)^2=0\end{matrix}\right.\Leftrightarrow x=y=-5\)