PT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
14 tháng 9 2021
\(M+N=3xyz-2x^2+5xy+5x^2+xyz-5y+3-2y=3x^2+4xyz+5xy-7y+3\)
\(N-M=5x^2+xyz-5y+3-2y-3xyz+2x^2-5xy=7x^2-2xyz-5xy-7y+3\)
TM
1
4 tháng 10 2021
b) \(16x-5x^2-3=5x\left(3-x\right)-\left(3-x\right)=\left(3-x\right)\left(5x-1\right)\)
c) \(2x^2+3x-5=2x\left(x-1\right)+5\left(x-1\right)=\left(x-1\right)\left(2x+5\right)\)
d) \(2x^2+3x-5=2x\left(x-1\right)+5\left(x-1\right)=\left(x-1\right)\left(2x+5\right)\)
CM
8 tháng 11 2017
Lời giải
Ta có
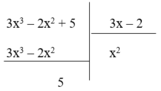
Vì phần dư R = 5 ≠ 0 nên phép chia đa thức 3 x 3 – 2 x 2 + 5 cho đa thức 3x – 2 là phép chia có dư. Do đó (I) sai
Lại có
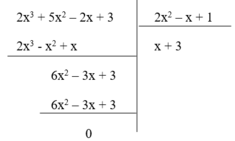
Nhận thấy phần dư R = 0 nên phép chia đa thức ( 2 x 3 + 5 x 2 – 2x + 3) cho đa thức (2 x 2 – x + 1) là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: D
H
2
29 tháng 10 2021
\(2x^3+5x^2-2x+a=x\left(2x^2-x+1\right)+3\left(2x^2-x+1\right)-3+a\)
\(=\left(2x^2-x+1\right)\left(x+3\right)-3+a⋮\left(2x^2-x+1\right)\)
\(\Rightarrow-3+a=0\Rightarrow a=3\)
29 tháng 10 2021
\(2x^3+5x^2-2x+a⋮2x^2-x+1\)
\(\Leftrightarrow2x^3-x^2+x+6x^2-3x+3+a-3⋮2x^2-x+1\)
\(\Leftrightarrow a-3=0\)
hay a=3
LV
1
21 tháng 12 2022
a: Khi x=-1 thì B=2*(-1)^2+1+1=4
b: Để A chia hết cho B thì
\(2x^3-x^2+x+6x^2-3x+3+a-3⋮2x^2-x+1\)
=>a-3=0
=>a=3
c: Để B=1 thì 2x^2-x=0
=>x=0 hoặc x=1/2
\(Q-\left(5x^2-xyz\right)=xy+2x^2-3xyz+5\)
\(\Leftrightarrow Q=xy+2x^2-3xyz+5+5x^2-xyz\)
\(\Leftrightarrow Q=7x^2+xy-4xyz+5\)
\(Q-\left(5x^2-xyz\right)=xy+2x^2-3xyz+5\\ Q=xy+2x^2-3xyz+5+5x^2-xyz\\ Q=7x^2+xy-4xyz+5\)