Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: 23 vị trí; 0,6mm.
Cách 1:
- Vân sáng của i1 trùng với vân tối của i2 →2i1 = 0,6mm; i2 = 0,4; i0 = 1,2mm;
- Ta có kM = -4,6; kN = 18,3. Số giá trị k bán nguyên là : 17,5 + 4,5 + 1 = 23 giá trị.
Cách 2:
+ Vân sáng của λ1 trùng với vân sáng của λ2: \(\frac{k_1}{k_2}=\frac{i_1}{i_2}=\frac{4}{3}\)
\(\Rightarrow\) Vân sáng có tọa độ 4ki1 của λ1 trùng với vân sáng có tọa độ 3ki2của λ2
\(\Rightarrow\) Vân sáng có tọa độ 2ki1 của λ1 trùng với vân sáng có tọa độ 1,5 ki2của λ2 (k lẻ)
\(\Rightarrow\) xtrùng = \((k+\frac{1}{2})4i_1(mm) \Rightarrow 5,5\leq(k+\frac{1}{2})4i_1\leq 2,2.10\)
\(\Leftrightarrow{-5,08}\leq{k}\leq{17,8}\)
\(\Rightarrow\) có 23 vị trí thỏa mãn.
Khoảng cách gần nhất từ điểm thỏa mãn đến vân trung tâm tương ứng với k = 0
xmin = 0,5.4i1 = 0,6 (mm)

Đáp án B
Ban đầu, tại M là vân sáng bậc 2 nên: 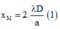
Sau khi dịch màn xa thêm một đoạn 50/3 cm theo phương vuông góc với mặt phẳng hai khe thì tại M là vị trí vân tối thứ 2 nên:
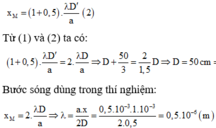

Cách giải: Đáp án D
Ta có

Vậy tại M lúc sau phải là vị trí của vân tối của λ2.Từ kết quả trên ta suy ra: MN = 10i1 =14i2 .Vậy trên đoạn MN có 15 vân tối.

Chọn D.
Với bức xạ λ vị trí vân sáng bậc k = 3, ta có x k = k λD a . Với bức xạ λ' vị trí vân sáng bậc k', ta có x k ' = k ' λ ' D a . Hai vân sáng này trùng nhau ta suy ra xk = xk’ tương đương với kλ = k’λ’ tính được λ’ = 0,6μm

\(\lambda_1=\dfrac{ai}{D}=0,4\mu m\)
Tại vị trí vân sáng bậc 3 của \(\lambda_1 \) ta thấy một vân sáng \(\lambda_2\)
\(\Rightarrow 3i_1=ki_2\)
\(\Rightarrow 3 \lambda_1=k.\lambda_2\)
\(\Rightarrow \lambda_2= \dfrac{3.0,4}{k}=\dfrac{1,2}{k}\)
Do \(\lambda_2 > \lambda_2 \Rightarrow k < 3\)
Vì là vân sáng nên k =2 \(\Rightarrow \lambda_2=0,6\mu m\)
k=2 nên vân sáng bậc 2
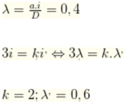
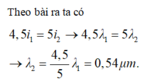

Tại vân tối thứ k của 1 bức xạ nào đó có N vân sáng, ta có: \(x=(k+0,5)i=k'.i'\)(*)
Trong môi trường chiết suất n thì bước sóng, khoảng vân giảm đi n lần.
Khi đó, \(i=2i_1;i'=2i_1'\)
Thay vào (*) ta được: \(x=(2k+1)i_1=2k'i_1'\)(**)
Biểu thức (**) đều là điều kiện cho vân sáng.
Như vậy, ta sẽ có (N+1) vân sáng.