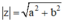Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Mỗi biểu thức dạng a+bi, trong đó a, b ∈ R, i2= -1 được gọi làm một số phức.
- Với số phức z = a + bi, ta gọi a là phần thực, số b gọi là phần ảo của z.
- Ta có z = a + bi thì môdun của z là |z|=|a+bi|=√a2+b2

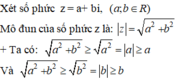
Vậy với mọi số phức thì phần thực và phần ảo của nó không vượt quá mô đun của nó.

Chọn D.
Giả sử z = x + yi; từ giả thiết : ![]()
Nên ( x + yi) 3+ 12i = x - yi
Hay x3 - 3xy2+ ( 3x2y - y3 +12) i = x - yi
Ta có hệ phương trình là x3 - 3xy2 = x (1) và 3x2y - y3 + 12 = - y ( 2)
Do x > 0 nên từ (1) x2 = 3y2+ 1. Thế vào (2) ta được:
3( 3y2 + 1) y - y3 + 12 = -y
Hay 2y3+ y + 3 = 0 (3)
Giải phương trình (3) ta được y = -1; x2 = 4. Do x > 0 nên x = 2.
Vậy z = 2 - i và ![]()

Chọn A.
Gọi số phức cần tìm là z = x = yi.
Ta có:
![]() hay x2 + y2 = 25 (*)
hay x2 + y2 = 25 (*)
Mặt khác: Số phức có phần thực của nó bằng 2 lần phần ảo nên x = 2y
thay vào phương trình (*) ta được: 5y2 = 25 hay ![]()
Vậy số phức cần tìm là: ![]()

a) Đường phân giác của góc phần tư thứ nhất và góc pần tư thứ ba.
b) Đường phân giác của góc phần tư thứ hai và góc phần tư thứ tư.
c) Đường thẳng y = 2x + 1
d) Nửa đường tròn tâm O bán kính bằng 1, nằm bên phải trục Oy.

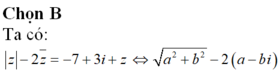
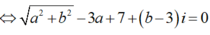
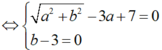
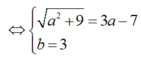
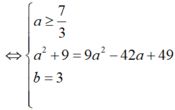
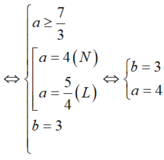
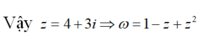
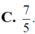
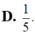

Mỗi số phức là một biểu thức z = a + bi với a, b ∈ R, i 2 = -1
- Số thực a là phần thực của số phức: z = a + bi
- Số thực b là phần ảo của số phức z = a + bi
- Môđun của số phức z = a + bi là