Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bất phương trình tương đương với 3 . 3 2 x - 10 . 3 x + 3 ≤ 0
Đặt t = 3 x > 0 Bất phương trình trở thành 3 t 2 - 10 t + 3 ≤ 0 ⇔ 1 3 ≤ t ≤ 3 .
Với 1 3 ≤ t ≤ 3 , ta được 1 3 ≤ 3 x ≤ 3 ⇔ - 1 ≤ x ≤ 1
Do đó tập nghiệm của bất phương trình là S = [ -1;1 ]
Vậy b - a = 2
Đáp án C

Đáp án B
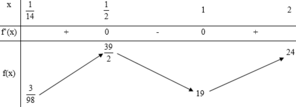
log 2 ( m x − 6 x 3 ) + log 1 2 ( − 14 x 2 + 29 x − 2 ) = 0 , ( 1 14 < x < 2 ) ⇔ log 2 ( m x − 6 x 3 ) − 14 x 2 + 29 x − 2 = 0 ⇔ m x − 6 x 3 + 14 x 2 − 29 x + 2 = 0 ⇔ 6 x 3 − 14 x 2 + 29 x − 2 x = m y = 6 x 3 − 14 x 2 + 29 x − 2 x ⇒ y ' = 12 x 3 − 14 x 2 + 2 x 2 y ' = 0 ⇔ x = − 1 3 ( L ) x = 1 2 x = 1 y ( 1 2 ) = 39 2 , y ( 1 ) = 19 ⇒ H = 39 2 − 19 = 1 2

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0 ⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0 ⇔ x 2 - ( m - 1 ) x + 2 m - 2 m 2 = 0 ( x - m ) ( x + 2 m ) > 0 ⇔ [ x = 2 m x = 1 - m x - m x + 2 m > 0
Điều kiện để pt đã cho có 2 nghiệm ⇔ 4 m 2 > 0 x - m x + 2 m > 0 ⇔ m ∈ - 1 ; 1 2 \ 0
Khi đó x 1 2 + x 2 2 > 1 ⇔ 4 m 2 + 1 - m 2 > 1 ⇔ 5 m 2 - 2 m > 0 ⇔ [ m > 2 5 m < 0
Do đó S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2

Đáp án A
Điều kiện: x ≥ − 1 ta có hệ phương trình:
x + 1 < 2 x x + 4 < 2 x 2 + 3 ⇔ 2 x 2 − x − 1 < 0
nên ta có lập luận sau
Vế phải bất phương trình:
g x = 6 x 2 − 3 x − 3 = 3 2 x 2 − x − 1 ⇒ g x > 0 ⇔ x ∈ − ∞ ; − 1 2 ∪ 1 ; + ∞ g x ≤ 0 ⇔ x ∈ − 1 2 ; 1
+) Với x>1 thì:
0 < x + 4 < 2 x 2 + 3 0 < x + 1 < 2 x ⇒ x + 4 x + 1 < 2 x 2 x 2 + 3 ⇒ V T < 0 , V P > 0 ⇒ B P T v ô n g h i ệ m .
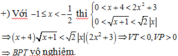
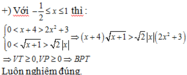
Vật tập nghiệm của bất phương trình là:
a ; b = − 1 2 ; 1 ⇒ 2 a + b = 2. − 1 2 + 1 = 0

Chọn đáp án A
Điều kiện: 1 ≤ x ≤ 3
Bất phương trình
![]() (1)
(1)
Xét hàm số f t = t 2 + 2 + t với t ≥ 0
Ta có
![]()
nên hàm số đồng biến trên [ 0 ; + ∞ ) .
Khi đó (1) ⇔ f x - 1 > f 3 - x
![]()
Kết hợp với điều kiện, tập nghiệm của bất phương trình là S = ( 2 ; 3 ]
Vậy a = 2 , b = 3 ⇒ b - a = 1
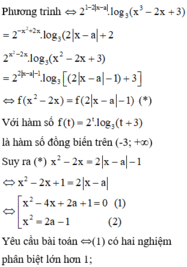
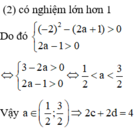

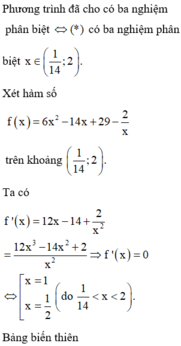

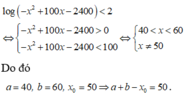
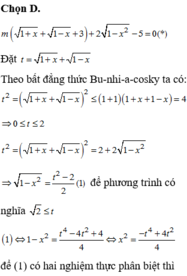

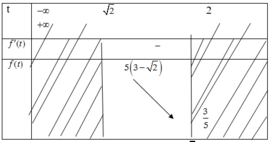
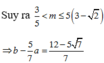
Chọn đáp án A