Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương pháp:
Đưa phương trình về dạng tích, giải phương trình tìm nghiệm và tìm điều kiện để bài toán thỏa.
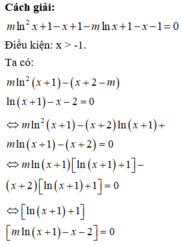
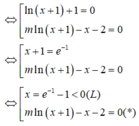

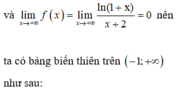
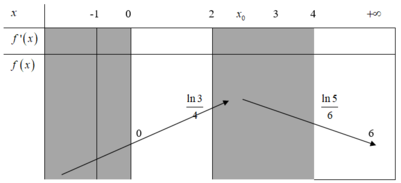


Đáp án A.
Phương trình đã cho tương đương với:
2 x 2 + m x + 1 = x 2 + 6 x + 9 x ≥ − 3 ⇔ x 2 + m − 6 x − 8 = 0 1 x ≥ − 3
Để phương trình có hai nghiệm phân biệt thì (1) phải có 2 nghiệm phân biệt x 2 > x 1 ≥ − 3
⇔ Δ > 0 x 1 + x 2 ≥ − 6 x 1 + 3 x 2 + 3 ≥ 0 ⇔ m − 6 2 + 32 > 0 − m − 6 ≥ − 6 − 8 + 3. − m + 6 + 9 ≥ 0 ⇔ 6 − m ≥ − 6 19 − 3 m ≥ 0 ⇔ m ≤ 12 m ≤ 19 3 ⇔ m ≤ 19 3
Do đó
a b = 19 3 ⇒ a = 19 b = 3 ⇒ B = a 2 − b 3 = 19 2 − 3 3 = 334.

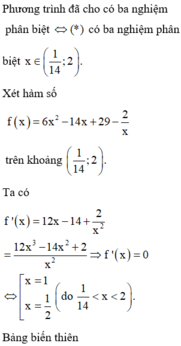


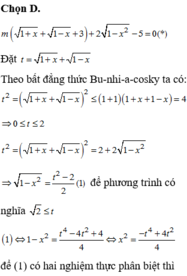



Đáp án B
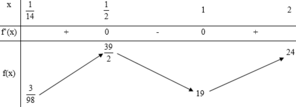
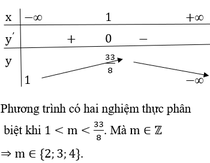
log 2 ( m x − 6 x 3 ) + log 1 2 ( − 14 x 2 + 29 x − 2 ) = 0 , ( 1 14 < x < 2 ) ⇔ log 2 ( m x − 6 x 3 ) − 14 x 2 + 29 x − 2 = 0 ⇔ m x − 6 x 3 + 14 x 2 − 29 x + 2 = 0 ⇔ 6 x 3 − 14 x 2 + 29 x − 2 x = m y = 6 x 3 − 14 x 2 + 29 x − 2 x ⇒ y ' = 12 x 3 − 14 x 2 + 2 x 2 y ' = 0 ⇔ x = − 1 3 ( L ) x = 1 2 x = 1 y ( 1 2 ) = 39 2 , y ( 1 ) = 19 ⇒ H = 39 2 − 19 = 1 2