Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay CP = 13,394 vào (1) ta có:
AP = 13,394.cotg 20 ° ≈ 36,801 (cm)
Thay CP = 13,394 vào (2) ta có:
BP = 13,394.cotg 30 ° ≈ 27,526 (cm)

Tính góc A (= 130 độ ). tam giác ACP vuông tại P => AP = cot A .CP (1)
tam giác BCP vuông tại P => BP = cot B . CP (2)
(1) +(2) => AP + BP =cot A .CP +cot B . CP
<=> AB = CP( cot A + cot B)
<=>60= CP ( cot 130 + cot 20 )
=> CP xấp xỉ 31.4
từ đó có thể dễ dàng tính ra AP và BP

trong tam giac ABH co\(AH=AB\cdot\sin B\) \(\Rightarrow AH=60\cdot\sin30=30\)
trong tam giac AHC co \(\sin C=\frac{AH}{AC}\Rightarrow AC=\frac{30}{\sin130}\approx39\)(vi \(gocC=180-20-30=130\)
TRONG TAM GIAC APC CO\(PC=AC\cdot\sin A=39\cdot\sin20\approx13,34\)
\(AP=\cos A\cdot39\approx36,65\)
\(\Rightarrow AP+BP=AB\Rightarrow BP=60-36.65=23.35\)

b) Xét ΔMEB và ΔMCF có
\(\widehat{MEB}=\widehat{MCF}\left(=\widehat{AEF}\right)\)
\(\widehat{M}\) chung
Do đó: ΔMEB\(\sim\)ΔMCF(g-g)
Suy ra: \(\dfrac{ME}{MC}=\dfrac{MB}{MF}\)
hay \(ME\cdot MF=MB\cdot MC\)
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AFE}=\widehat{ABC}\)(hai góc tương ứng)
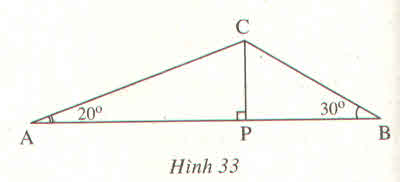

Đặt AP=x suy ra BP=60-x.Ta có phương trình
xtg\(20^0\)=(60-x)tg\(30^0\)
Đ/s:AP ≈36,801cm;BP=23,119cm;CP=13,396cm
Tham khảo nha