Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phần bên trên giải thích rồi còn gì
n + n - 1 + n - 2 + n - 3 + .... + 1
Tổng của dãy số hơn kém 1 đơn vị lùi từ n về 1
T = (Số đầu - số cuối) . số số hạng rồi chia 2
tức là \(\dfrac{\left(n-1\right).n}{2}\)

TXĐ: `D=RR\\{π/2+kπ ; -π/4 +kπ}`
Mà `-π/2+k2π` và `π/2+k2π \in π/2 +kπ`
`=>` Không nằm trong TXĐ.

\(\Leftrightarrow\left[{}\begin{matrix}3x=x+k2\pi\\3x=-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\)
\(0< \dfrac{k\pi}{2}< 2017\pi\Rightarrow0< k< 4034\)
Có \(4033\) nghiệm (tất cả các đáp án đều sai)

k ở đây được hiểu là "một số nguyên bất kì", giống hay khác nhau đều được
Ví dụ:
\(sinx=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Thì "k" trong \(\dfrac{\pi}{6}+k2\pi\) và "k" trong \(\dfrac{5\pi}{6}+k2\pi\) không liên quan gì đến nhau (nó chỉ là 1 kí hiệu, có thể k trên bằng 0, k dưới bằng 100 cũng được, không ảnh hưởng gì, cũng có thể 2 cái bằng nhau cũng được).
Khi người ta ghi 2 nghiệm đều là "k2pi" chủ yếu do... lười biếng (kiểu như mình). Trên thực tế, rất nhiều tài liệu cũ họ ghi các kí tự khác nhau, ví dụ 1 nghiệm là \(\dfrac{\pi}{6}+k2\pi\), 1 nghiệm là \(\dfrac{5\pi}{6}+n2\pi\) để tránh học sinh phát sinh hiểu nhầm đáng tiếc rằng "2 cái k phải giống hệt nhau về giá trị".

1/
Bạn chỉ cần tìm sin, cos trong \(\left[0;2\pi\right]\) là đủ (vì cả 2 hàm đều tuần hoàn với chu kì \(2\pi\))
Đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\) với \(a\in\left[0;2\pi\right]\)
\(\Rightarrow4sina.cosa\left(2cos^2a-1\right)=1\)
\(\Leftrightarrow2sin2a.cos2a=1\Leftrightarrow sin4a=1\)
\(\Rightarrow4a=\frac{\pi}{2}+k2\pi\Rightarrow a=\frac{\pi}{8}+\frac{k\pi}{2}\)
\(\Rightarrow0\le\frac{\pi}{8}+\frac{k\pi}{2}\le2\pi\Rightarrow a=\left\{\frac{\pi}{8};\frac{5\pi}{8};\frac{9\pi}{8};\frac{13\pi}{8};\frac{17\pi}{8}\right\}\)
\(\Rightarrow\left(x;y\right)=\left(sin\frac{\pi}{8};cos\frac{\pi}{8}\right);\left(sin\frac{5\pi}{8};cos\frac{5\pi}{8}\right)...\)
2.
\(sinx=\frac{1}{3}\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\frac{1}{3}\right)+k2\pi\\x=\pi-arcsin\left(\frac{1}{3}\right)+l2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\frac{1}{3}\right)\\x=\pi-arcsin\left(\frac{1}{3}\right)\end{matrix}\right.\)
(Vì \(0< \frac{1}{3}< 1\) nên \(0< arcsin\left(\frac{1}{3}\right)< \frac{\pi}{2}\) do đó nếu \(k>0\Rightarrow arcsin\left(\frac{1}{3}\right)+k2\pi>2\pi\) ; nếu \(k\le-1\Rightarrow arcsin\left(\frac{1}{3}\right)+k2\pi\le-\frac{3\pi}{2}\) đều ko thuộc \(\left[0;\pi\right]\Rightarrow k=0\).
Tương tự với \(l\))
Cho mình hỏi sao từ 0 < 1/3 < 1 thì suy ra đc 0 < arcsin (1/3) < pi/2 vậy?

\(\Leftrightarrow cosx+sinx+\dfrac{cosx+sinx}{sinx-cosx}=0\)
\(\Leftrightarrow\left(cosx+sinx\right)\left(1+\dfrac{1}{sinx-cosx}\right)=0\)
Chuyển vế rồi đặt nhân tử chung thôi em

Lý do gì em lại tin 1 cuốn sách có nguồn từ đâu đó hơn là tài liệu chính thống của BGD sử dụng trong đào tạo?
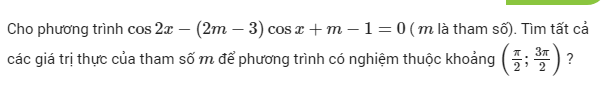

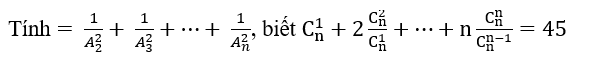
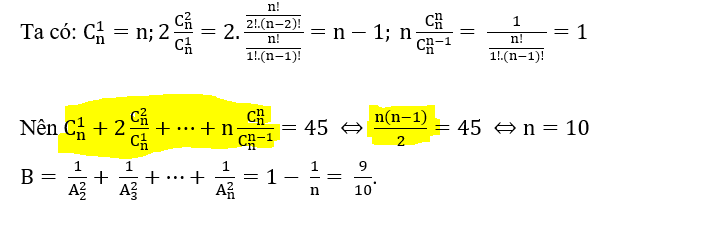
 Sách cũng có nói Parabol k thể được gọi là đồ thị hàm số. Mình hơi thắc mắc vì ở trường thầy cô đều nói là đồ thị hàm số bậc 1,2. Như vậy hàm số bậc 1,2 khi vẽ ra hệ descart có được gọi là đồ thị hs k ạ. Cao nhân giải đáp giúp mình với
Sách cũng có nói Parabol k thể được gọi là đồ thị hàm số. Mình hơi thắc mắc vì ở trường thầy cô đều nói là đồ thị hàm số bậc 1,2. Như vậy hàm số bậc 1,2 khi vẽ ra hệ descart có được gọi là đồ thị hs k ạ. Cao nhân giải đáp giúp mình với
\(\Leftrightarrow2cos^2x-1-\left(2m-3\right)cosx+m-1=0\)
\(\Leftrightarrow2cos^2x-\left(2m-3\right)cosx+m-2=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(cosx-m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=m-2\end{matrix}\right.\)
Do \(cosx=\dfrac{1}{2}\Rightarrow x=\dfrac{\pi}{3}+k2\pi\) ko có nghiệm thuộc khoảng đã chi
\(\Rightarrow cosx=m-2\) có nghiệm thuộc \(\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\)
Ta có \(x\in\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\Rightarrow cosx\in\left(-1;0\right)\)
\(\Rightarrow-1< m-2< 0\)
\(\Rightarrow1< m< 2\)