Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Đạo hàm: y’ = x2 + 6x.
k = -9 ⇔ y’(xo) = -9 ⇔ xo2 + 6xo = -9 ⇔ (xo + 3)2 ⇔ xo = -3 ⇒ yo = 16
Phương trình tiếp tuyến cần tìm là (d): y = -9(x + 3) + 16 ⇔ y – 16 = -9(x + 3).

- Tập xác định: D = R
- Đạo hàm: y ' = x 2 + 6 x .
- Tiếp tuyến có hệ số góc k = -9 nên:
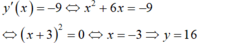
- Phương trình tiếp tuyến cần tìm là:
y = - 9(x + 3) + 16 hay y = -9x - 11
Chọn A.

- Tập xác định: D = R.
- Đạo hàm: y ' = x 2 + 6 x .
- Tiếp tuyến tại điểm M ( x 0 , y 0 ) của đồ thị hàm số có hệ số góc là – 9
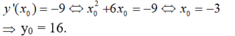
- Do đó, phương trình tiếp tuyến của đồ thị hàm số tại điểm M(-3, 16) là:
y = -9(x + 3) + 16 hay y = -9x – 11.
Chọn A.

cos2(x + kπ) = cos(2x + k2π) = cos2x, k ∈ Z.
Vậy hàm số y = cos 2x là hàm số chẵn, tuần hoàn, có chu kì là π.
Đồ thị hàm số y = cos2x
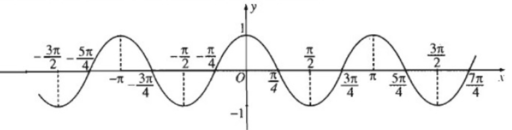
Đồ thị hàm số y = |cos2x|
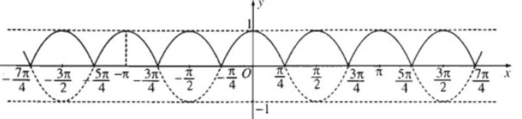

a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
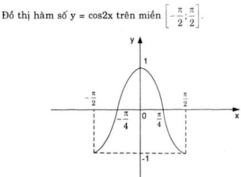
Từ đó suy ra
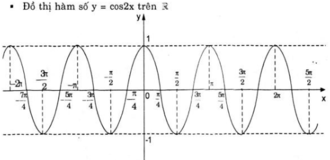
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
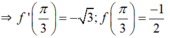
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
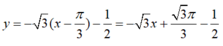
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
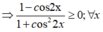
⇒ 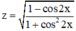 luôn xác định với mọi x ∈ R.
luôn xác định với mọi x ∈ R.
 Sách cũng có nói Parabol k thể được gọi là đồ thị hàm số. Mình hơi thắc mắc vì ở trường thầy cô đều nói là đồ thị hàm số bậc 1,2. Như vậy hàm số bậc 1,2 khi vẽ ra hệ descart có được gọi là đồ thị hs k ạ. Cao nhân giải đáp giúp mình với
Sách cũng có nói Parabol k thể được gọi là đồ thị hàm số. Mình hơi thắc mắc vì ở trường thầy cô đều nói là đồ thị hàm số bậc 1,2. Như vậy hàm số bậc 1,2 khi vẽ ra hệ descart có được gọi là đồ thị hs k ạ. Cao nhân giải đáp giúp mình với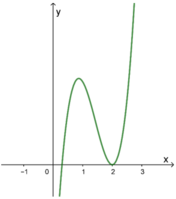



 \
\






Lý do gì em lại tin 1 cuốn sách có nguồn từ đâu đó hơn là tài liệu chính thống của BGD sử dụng trong đào tạo?
Cuốn sách nổi tiếng ik ạ!! Nói về giải tích của James stewart hầu hết các thí sinh thi IPHO đều học quyển này.