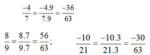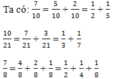Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giải:
a) Gọi dãy đó là A, ta có:
\(A=\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2014}}\)
\(2A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2013}}\)
\(2A-A=\left(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2013}}\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2014}}\right)\)
\(A=\dfrac{1}{2}-\dfrac{1}{2^{2014}}\)
Vì \(\dfrac{1}{2}< 1;\dfrac{1}{2^{2014}}< 1\) nên \(\dfrac{1}{2}-\dfrac{1}{2^{2014}}< 1\)
\(\Rightarrow A< 1\)
b) \(A=\dfrac{10^{11}-1}{10^{12}-1}\) và \(B=\dfrac{10^{10}+1}{10^{11}+1}\)
Ta có:
\(A=\dfrac{10^{11}-1}{10^{12}-1}\)
\(10A=\dfrac{10^{12}-10}{10^{12}-1}\)
\(10A=\dfrac{10^{12}-1+9}{10^{12}-1}\)
\(10A=1+\dfrac{9}{10^{12}-1}\)
Tương tự:
\(B=\dfrac{10^{10}+1}{10^{11}+1}\)
\(10B=\dfrac{10^{11}+10}{10^{11}+1}\)
\(10B=\dfrac{10^{11}+1+9}{10^{11}+1}\)
\(10B=1+\dfrac{9}{10^{11}+1}\)
Vì \(\dfrac{9}{10^{12}-1}< \dfrac{9}{10^{11}+1}\) nên \(10A< 10B\)
\(\Rightarrow A< B\)



Các phân số đều tối giản. Mẫu số chung là BCNN(7, 9, 21) = 32.7 = 63
Thừa số phụ của 7 là 9, của 9 là 7, của 21 là 3. Do đó: