Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mặt cầu (S) có tâm \(I\left(1;0;0\right)\) bán kính \(R=1\)
Do mặt phẳng (P) song song với (Q)
\(\Rightarrow\) Phương trình (P) có dạng: \(5x-12z+a=0\)
Do (P) tiếp xúc với (S) \(\Rightarrow d\left(I;\left(P\right)\right)=R\)
\(\Rightarrow\frac{\left|5.1+0.0-12.0+a\right|}{\sqrt{5^2+0^2+\left(-12\right)^2}}=1\Leftrightarrow\left|a+5\right|=13\Rightarrow\left[{}\begin{matrix}a=8\\a=-18\end{matrix}\right.\)
\(\Rightarrow\) Có hai pt (P) thỏa mãn: \(\left[{}\begin{matrix}5x-12z+8=0\\5x-12z-18=0\end{matrix}\right.\)
Đáp án A
Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của tam giác A’B’C’ cùng nằm trên một đường thẳng đi qua O. Viết phương trình đường thẳng đó.
Tọa độ điểm \(G\) là \(G\left(\dfrac{6+0+0}{3},\dfrac{0+4+0}{3},\dfrac{0+0+3}{3}\right)\) suy ra \(G\left(2,\dfrac{4}{3},1\right)\).
\(\overrightarrow{AB}=\left(-2,3,0\right),\overrightarrow{BC}=\left(0,-3,4\right),\overrightarrow{CA}=\left(2,0,-4\right)\)
Đặt \(H\left(a,b,c\right)\).
Vì \(H\) là trực tâm tam giác \(ABC\) nên
\(\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{CA}=0\\\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AH}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3b+4c=0\\2a-4c=0\\12\left(a-2\right)+8b+6c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{72}{61}\\b=\dfrac{48}{61}\\c=\dfrac{36}{61}\end{matrix}\right.\) suy ra \(H\left(\dfrac{72}{61},\dfrac{48}{61},\dfrac{36}{61}\right)\).
\(\overrightarrow{OG}=\left(2,\dfrac{4}{3},1\right)\)
Đường thẳng qua OG: \(\left\{{}\begin{matrix}x=2t\\y=\dfrac{4}{3}t\\z=t\end{matrix}\right.\).
Bằng cách thử trực tiếp, ta thấy H nằm trên đường thẳng OG.
Mặt phẳng nhận u → và v → là vec tơ chỉ phương
⇒ nhận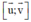 
= (2.1 – 1.0 ; 1.(-3) – 3.1 ; 3.0 – (-3).2) = (2; -6; 6) là vec tơ pháp tuyến.
Mặt phẳng đi qua A(0 ; -1 ; 2) nên có phương trình :
2(x – 0) – 6(y + 1) + 6(z – 2) = 0
⇔ 2x – 6y + 6z – 18 = 0
⇔ x – 3y + 3z – 9 = 0.
Bán kính mặt cầu: \(R=\sqrt{1^2+\left(-2\right)^2+1^2+8}=\sqrt{14}\)
Tâm mặt cầu: \(I\left(1;-2;1\right)\)
\(\Rightarrow d\left(I;\left(Q\right)\right)=\sqrt{R^2-\left(\frac{R}{2}\right)^2}=\frac{\sqrt{42}}{2}\)
Do (Q) song song (P) nên pt (Q) có dạng: \(2x+3y+z+d=0\)
Áp dụng công thức khoảng cách:
\(d\left(I;\left(Q\right)\right)=\frac{\left|2-6+1+d\right|}{\sqrt{2^2+3^2+1}}=\frac{\sqrt{42}}{2}\)
\(\Leftrightarrow\left|d-3\right|=7\sqrt{3}\Rightarrow\left[{}\begin{matrix}d=3+7\sqrt{3}\\d=3-7\sqrt{3}\end{matrix}\right.\)
Có 2 mặt phẳng thỏa mãn: \(\left[{}\begin{matrix}2x+3y+z+3+7\sqrt{3}=0\\2x+3y+z+3-7\sqrt{3}=0\end{matrix}\right.\)
Nếu đề là $f(x)=\frac{x-3}{x^2+2x-3}$ thì giải như sau:
Ta có:
\(F(x)=\int f(x)dx=\int \frac{x-3}{x^2+2x-3}dx=\int \frac{\frac{-1}{2}(x+3)+\frac{3}{2}(x-1)}{(x-1)(x+3)}dx\)
\(=-\frac{1}{2}\int \frac{dx}{x-1}+\frac{3}{2}\int \frac{dx}{x+3}=\frac{-1}{2}\ln |x-1|+\frac{3}{2}\ln |x+3|+c\)
\(F(0)=\frac{-1}{2}\ln |0-1|+\frac{3}{2}\ln |0+3|+c=0\Rightarrow c=\frac{-3}{2}\ln 3\)
\(F(2)=\frac{-1}{2}\ln |2-1|+\frac{3}{2}\ln |2+3|-\frac{3}{2}\ln 3=\frac{3}{2}\ln \frac{5}{3}\)
Nhi Le: Ý bạn là \(f(x)=\frac{x-3}{x^2+2x-3}\) hay $f(x)=x-\frac{3}{x^2+2x-3}$ vậy
Cách 1:
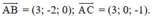
Mặt phẳng (R) đi qua ba điểm A, B, C nhận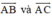 
là hai vec tơ chỉ phương
⇒ Nhận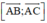 
= ((-2).(-1) – 0; 0.3 – 3.(-1); 3.0 – 3.(-2)) = (2; 3; 6) là vec tơ pháp tuyến.
(R) đi qua A(-3; 0; 0) nên có phương trình:
2(x + 3) + 3y + 6z = 0
⇔ 2x + 3y + 6z + 6 = 0.
Cách 2 :
(R) đi qua A(-3 ; 0 ; 0) ; B(0 ; -2 ; 0) ; C(0 ; 0 ; -1) nên có phương trình đoạn chắn là :
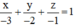
⇔ 2x + 3y + 6z + 6 = 0.
\(x.0,\left(2\right)+0,\left(3\right)=0,\left(77\right)\)
\(\Rightarrow x.\frac{2}{9}+\frac{3}{9}=\frac{7}{9}\)
\(\Rightarrow\frac{2x}{9}=\frac{7}{9}-\frac{3}{9}\)
\(\Rightarrow\frac{2x}{9}=\frac{4}{9}\)
\(\Rightarrow x=2\)
Vậy x = 2
\(OB=\sqrt{SB^2-SO^2}=\frac{a\sqrt{3}}{3}\) \(\Rightarrow OA=\sqrt{AB^2-OB^2}=\frac{a\sqrt{6}}{3}\)
Đặt hệ trục Oxyz vào hình chóp với \(Oz\) trùng tia \(OS\); \(Ox\) trùng tia OB, Oy trùng tia OA, \(\frac{a}{3}\) bằng 1 đơn vị độ dài
\(\Rightarrow S\left(0;0;\sqrt{6}\right)\); \(A\left(0;\sqrt{6};0\right);B\left(\sqrt{3};0;0\right);D\left(-\sqrt{3};0;0\right)\)
\(\Rightarrow\overrightarrow{SA}=\left(0;\sqrt{6};-\sqrt{6}\right)=\sqrt{6}\left(0;1;-1\right)\)
\(\overrightarrow{SB}=\left(\sqrt{3};0;-\sqrt{6}\right)=\sqrt{3}\left(1;0;-\sqrt{2}\right)\)
\(\overrightarrow{SD}=\left(-\sqrt{3};0;-\sqrt{6}\right)=-\sqrt{3}\left(1;0;\sqrt{2}\right)\)
\(\Rightarrow\overrightarrow{n_{\left(SAB\right)}}=\left[\overrightarrow{SA};\overrightarrow{SB}\right]=\left(\sqrt{2};1;1\right)\)
\(\overrightarrow{n_{\left(SAD\right)}}=\left[\overrightarrow{SA};\overrightarrow{SD}\right]=\left(\sqrt{2};-1;-1\right)\)
\(\Rightarrow cos\alpha=\frac{\left|2-1-1\right|}{\sqrt{2+1+1}\sqrt{2+1+1}}=0\Rightarrow\alpha=90^0\)
