Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 12 < 15 (*). Để có bất đẳng thức cùng chiều là 12a < 15a ta phải nhân cả hai vế của (*) với số dương. Vậy a là số dương.

a)12a<15a
Ta có:12<15 để có bất đẳng thức
12a<15a ta phải nhân cả 2 vế của bất đẳng thức 12<15 vs số a
Để đc bất đẳng thức cùng chiều thì a<0
b)4a<3a
Vì 4>3 và 4a<3a trái chiều.Để nhân 2 vế của bất đẳng thức 4>3 vs a đc bất đẳng thức trái chiều thì a<0
c)-3a>-5a
Từ -3 > -5 để có -3a > -5a thì a phải là số dương


Lời giải:
Để ý rằng 4n2+16n+7=(2n+1)(2n+7)4n2+16n+7=(2n+1)(2n+7)
Vì n∈N⇒2n+1,2n+7>1n∈N⇒2n+1,2n+7>1
Do đó, 4n2+16n+7∉P4n2+16n+7∉P với mọi số tự nhiên nn
Vậy không tìm được số nn thỏa mãn điều kiện đề bài
K MK NHÁ
#HC TỐT#
#TTV#
Đặt a+1=p suy ra:4a2+8a+5=4p2+1
6a2+12a+7=6p2+1
Do p là số nguyên tố nên thử chọn p
p=2 loại
p=3 loại
Ta được p=5
với p>5 thì p ko chia hết cho 5
suy ra p có dạng 5k+1, 5k+2,5k+3,5k+4(k trong N)
với 5k+1=p thì có : 4p2+1=100k2+40k+5 chia hết cho 5 loại
với 5k+2=p thì có : 6p2+1=150k2+120k+25 chia hết cho 5 loại
với p=5k+3 và 5k+4 tương tự
Suy ra p=5
Vậy a+1=p,a=4

b: \(=\left(a^2+5a+4\right)\left(a^2+5a+6\right)+1\)
\(=\left(a^2+5a\right)^2+10\left(a^2+5a\right)+25\)
\(=\left(a^2+5a+5\right)^2\)

Ta có: \(ab=cd\)
\(\Leftrightarrow\frac{a}{d}=\frac{c}{b}\)
Đặt \(\frac{a}{d}=\frac{c}{b}=k\) \(\left(k\inℕ\right)\)
\(\Rightarrow\hept{\begin{cases}a=dk\\c=bk\end{cases}}\)
Ta có: \(a^5+b^5+c^5+d^5\)
\(=d^5k^5+b^5+b^5k^5+d^5\)
\(=k^5\left(d^5+b^5\right)+\left(d^5+b^5\right)\)
\(=\left(k^5+1\right)\left(d^5+b^5\right)\) là hợp số
=> đpcm
Gọi \(\left(a,c\right)=k\), ta có \(a=ka',c=kc'\)và \(\left(a',c'\right)=1\)
Thay vào ab = cd được \(ka'b=kc'd\)nên \(a'b=c'd\)(*)
\(\Rightarrow a'b⋮c'\)mà\(\left(a',c'\right)=1\)nên \(b⋮c'\). Đặt \(b=c't\left(t\inℕ^∗\right)\), thay vào (*) được \(a'c't=c'd\Rightarrow a't=d\)
Do đó \(a^5+b^5+c^5+d^5=k^5a'^5+c'^5t^5+k^5c'^5+a'^5t^5\)\(=a'^5\left(k^5+t^5\right)+c'^5\left(k^5+t^5\right)=\left(a'^5+c'^5\right)\left(k^5+t^5\right)\)
Do a', c', k, t là các số nguyên dương nên \(a^5+b^5+c^5+d^5\)là hợp số (đpcm)
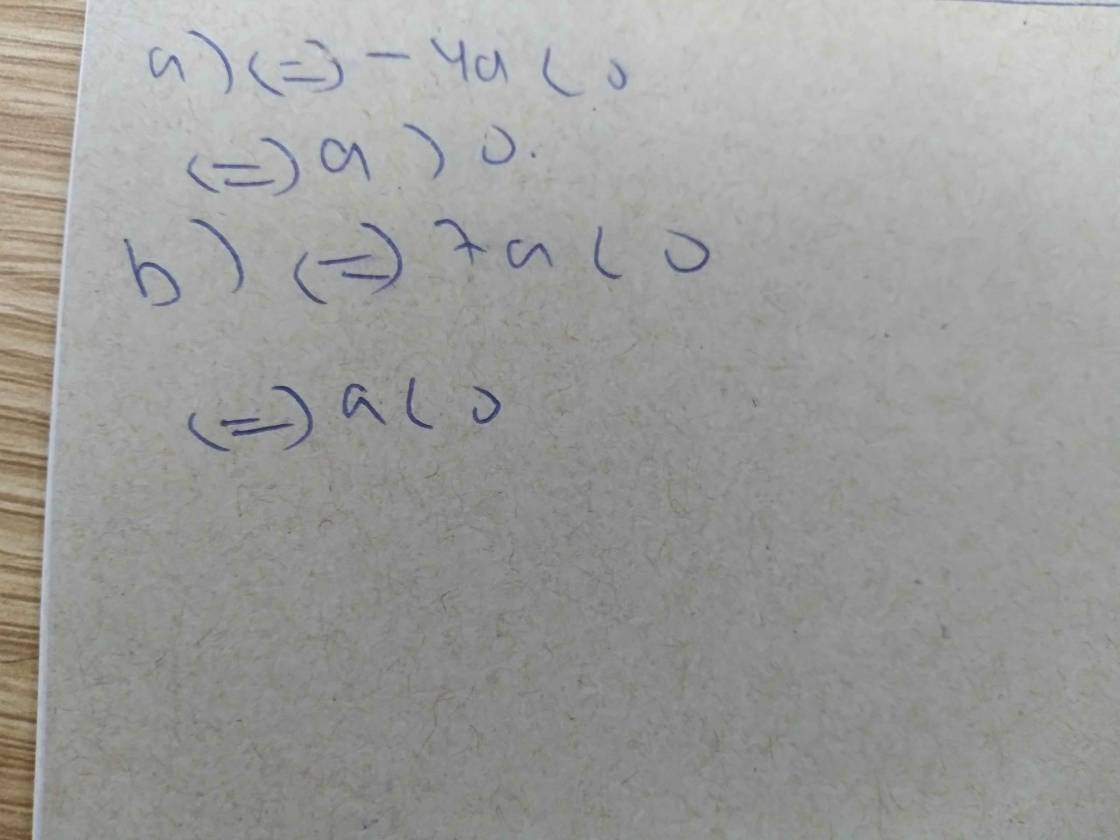
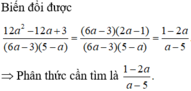
a) Do -8 < 4 nên a < 0 b) Do 5 ≤ 30 nên a ≥ 0
c) Do 6 < 12 nên a ≤ 0. d) Do -5 < 15 nên a < 0.