
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=a^4+a^3+a^2-a^3-a^2-a-5a^2-5a-5\)
\(M=a^2\left(a^2+a+1\right)-a\left(a^2+a+1\right)-5\left(a^2+a+1\right)\)
\(M=\left(a^2+a+1\right)\left(a^2-a-5\right)\)
M là số nguyên tố khi và chỉ khi \(a^2+a+1\) là SNT và \(a^2-a-5=1\)
\(\Rightarrow a^2-a-6=0\Rightarrow\left[{}\begin{matrix}a=3\\a=-2\left(loại\right)\end{matrix}\right.\)
Thay \(a=3\) vào ta được \(a^2+a+1=13\) là SNT (thỏa mãn)
Vậy \(a=3\)

Vì a
≠
±
3/2 nên
4
a
2
-
9
≠
0 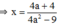
Vì a
≠
- 1 nên
3
a
3
+
3
≠
0 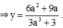
Do đó: 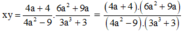
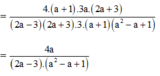

LEGGO chắc ghi nhầm ở chỗ \(4a^2+8a+4\) => sửa lại \(4a^2+8a+5\)
Không tồn tại số $a$ thỏa mãn điều kiện đề bài vì với mọi \(a\in\mathbb{N}\Rightarrow 4a^2+8a+4>2\) và \(4a^2+8a+4\vdots 2\) nên \(4a^2+8a+4\) không thể là số nguyên tố.

1.
\(p=2\Rightarrow p+6=8\) ko phải SNT (ktm)
\(\Rightarrow p>2\Rightarrow p\) lẻ \(\Rightarrow p^2\) lẻ \(\Rightarrow p^2+2021\) luôn là 1 số chẵn lớn hơn 2 \(\Rightarrow\) là hợp số
2.
\(a^2+3a=k^2\Rightarrow4a^2+12a=4k^2\)
\(\Rightarrow4a^2+12a+9=4k^2+9\Rightarrow\left(2a+3\right)^2=\left(2k\right)^2+9\)
\(\Rightarrow\left(2a+3-2k\right)\left(2a+3+2k\right)=9\)
\(\Leftrightarrow...\)

Biến đổi ta được: m = 7 ( a + 1 ) ( 2 a − 5 ) ( 2 a + 5 ) ; n = 3 a ( 2 a + 5 ) 5 ( a 3 + 1 )
⇒ A = mn = 21 a ( 2 a − 5 ) ( a 2 − a + 1 )
Lời giải:
Để ý rằng 4n2+16n+7=(2n+1)(2n+7)4n2+16n+7=(2n+1)(2n+7)
Vì n∈N⇒2n+1,2n+7>1n∈N⇒2n+1,2n+7>1
Do đó, 4n2+16n+7∉P4n2+16n+7∉P với mọi số tự nhiên nn
Vậy không tìm được số nn thỏa mãn điều kiện đề bài
K MK NHÁ
#HC TỐT#
#TTV#
Đặt a+1=p suy ra:4a2+8a+5=4p2+1
6a2+12a+7=6p2+1
Do p là số nguyên tố nên thử chọn p
p=2 loại
p=3 loại
Ta được p=5
với p>5 thì p ko chia hết cho 5
suy ra p có dạng 5k+1, 5k+2,5k+3,5k+4(k trong N)
với 5k+1=p thì có : 4p2+1=100k2+40k+5 chia hết cho 5 loại
với 5k+2=p thì có : 6p2+1=150k2+120k+25 chia hết cho 5 loại
với p=5k+3 và 5k+4 tương tự
Suy ra p=5
Vậy a+1=p,a=4