Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)((sqrt(14)-sqrt7)/(1-sqrt2)+(sqrt{15}-sqrt5)/(1-sqrt3)):1/(sqrt7-sqrt5)`
`=((sqrt7(sqrt2-1))/(1-sqrt2)+(sqrt5(sqrt3-1))/(1-sqrt3)).(sqrt7-sqrt5)`
`=(-sqrt7-sqrt5)*(sqrt7-sqrt5)`
`=-(sqrt7+sqrt5)(sqrt7+sqrt5)`
`=-(7-5)=-2`
`b)sqrt2+1/sqrt{5+2sqrt6}+2/sqrt{8+2sqrt{15}}`
`=sqrt2+1/sqrt{3+2sqrt{3}.sqrt2+2}+2/sqrt{5+2sqrt{5}.sqrt3+3}`
`=sqrt2+1/sqrt{(sqrt3+sqrt2)^2}+2/sqrt{(sqrt5+sqrt3)^2}`
`=sqrt2+1/(sqrt3+sqrt2)+2/(sqrt5+sqrt3)`
`=sqrt2+((sqrt3+sqrt2)(sqrt3-sqrt2))/(sqrt3+sqrt2)+((sqrt5+sqrt3)(sqrt5-sqrt3))/(sqrt5+sqrt3)`
`=sqrt2+sqrt3-sqrt2+sqrt5-sqrt3=sqrt5`
a) Ta có: \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{7}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}-\dfrac{\sqrt{5}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=-2\)
b) Ta có: \(\sqrt{2}+\dfrac{1}{\sqrt{5+2\sqrt{6}}}+\dfrac{2}{\sqrt{8+2\sqrt{15}}}\)
\(=\sqrt{2}+\dfrac{1}{\sqrt{3}+\sqrt{2}}+\dfrac{2}{\sqrt{5}+\sqrt{3}}\)
\(=\sqrt{2}+\sqrt{3}-\sqrt{2}+\sqrt{5}-\sqrt{3}\)
\(=\sqrt{5}\)

a) \(=2\sqrt{5}-3\sqrt{5}+\sqrt{5}-1=-1\)
b) \(=\left[\sqrt{14}+\dfrac{\sqrt{6}\left(\sqrt{2}+\sqrt{5}\right)}{\sqrt{2}+\sqrt{5}}\right].\sqrt{\left(\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{3}{2}}\right)^2}\)
\(=\left(\sqrt{14}+\sqrt{6}\right)\left(\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{3}{2}}\right)\)
\(=\sqrt{49}-\sqrt{21}+\sqrt{21}-\sqrt{9}\)
\(=7-3=4\)

Bạn chia nhỏ ra để nhận được câu tl sớm nhất nhé!Bạn đặt câu hỏi free mà để dày cộp như này khum ai dám làm =(((
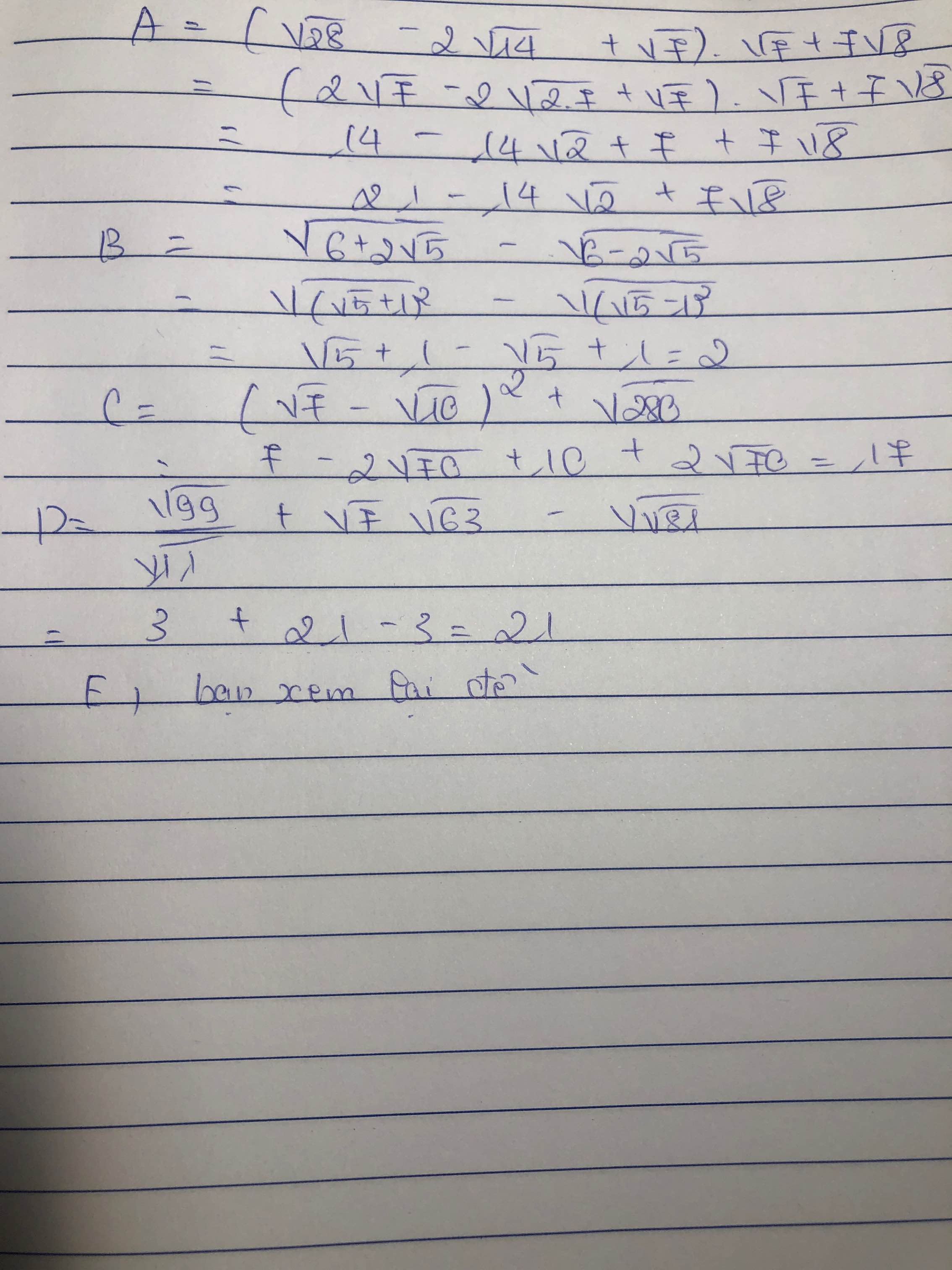
\(a,\dfrac{\sqrt{10}-\sqrt{15}}{\sqrt{8}-\sqrt{12}}\\ =\dfrac{\sqrt{2}.\sqrt{5}-\sqrt{3}.\sqrt{5}}{\sqrt{2}.\sqrt{4}-\sqrt{3}.\sqrt{4}}\\ =\dfrac{\sqrt{5}\left(\sqrt{2}-\sqrt{3}\right)}{\sqrt{4}\left(\sqrt{2}-\sqrt{3}\right)}\\ =\dfrac{\sqrt{5}}{\sqrt{2^2}}\\ =\dfrac{\sqrt{5}}{2}\)
\(b,\dfrac{\sqrt{15}-\sqrt{6}}{\sqrt{35}-\sqrt{14}}\\ =\dfrac{\sqrt{5}.\sqrt{3}-\sqrt{3}.\sqrt{2}}{\sqrt{5}.\sqrt{7}-\sqrt{7}.\sqrt{2}}\\ =\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}\left(\sqrt{5}-\sqrt{2}\right)}\\ =\dfrac{\sqrt{3}}{\sqrt{7}}\)
\(c,\dfrac{5+\sqrt{5}}{\sqrt{10}+\sqrt{2}}\\ =\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{2}\left(\sqrt{5}+1\right)}=\dfrac{\sqrt{5}}{\sqrt{2}}\)
\(a,=\dfrac{\sqrt{2}.\sqrt{5}-\sqrt{3}.\sqrt{5}}{2\sqrt{2}-2\sqrt{3}}\\ =\dfrac{\sqrt{5}.\left(\sqrt{2}-\sqrt{3}\right)}{2\left(\sqrt{2}-\sqrt{3}\right)}\\ =\dfrac{\sqrt{5}}{2}\)
\(b,=\dfrac{\sqrt{3}.\sqrt{5}-\sqrt{2}.\sqrt{3}}{\sqrt{5}.\sqrt{7}-\sqrt{2}.\sqrt{7}}\\ =\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}\left(\sqrt{5}-\sqrt{2}\right)}\\ =\dfrac{\sqrt{3}}{\sqrt{7}}=\dfrac{\sqrt{21}}{7}\)
\(c,=\dfrac{\sqrt{5}.\sqrt{5}+\sqrt{5}}{\sqrt{2}.\sqrt{5}+\sqrt{2}}\\ =\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{2}\left(\sqrt{5}+1\right)}\\ =\dfrac{\sqrt{5}}{\sqrt{2}}=\dfrac{\sqrt{10}}{2}\)