Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C.
Phương pháp
Sử dụng tính chất hai góc bù nhau cos x = cos π − x
Giải phương trình lượng giác cơ bản
Cách giải
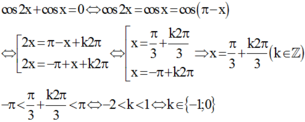
Vậy phương trình có 2 nghiệm thuộc − π ; π

Đáp án D
PT
⇔ 1 − 2 sin 2 x + 4 sin x + 5 = 0 ⇔ sin 2 x − 2 sin x − 3 = 0 ⇔ sin x = − 1 sin x = 3
⇒ sin x = − 1 ⇔ x = − π 2 + k 2 π k ∈ ℤ
Vì
x ∈ 0 ; 10 π ⇔ 0 < − π 2 + k 2 π < 10 π ⇔ 1 4 < k < 21 4 ⇒ k ∈ 1 ; 2 ; 3 ; 4 ; 5

Đáp án B
Ta có: P T ⇔ 4 c os 3 x − 3 cos x + 2 sin 2 x + 9 sin x − 5 = 0
⇔ cos x 4 c os 2 x − 3 + 2 sin 2 x + 9 sin x − 5 = 0 ⇔ cos x 1 − 4 sin 2 x + 2 sin x − 1 s inx + 5 = 0 ⇔ 2 sin x − 1 cos x + 2 sin x cos x + s inx + 5 = 0 ⇔ 2 sin x − 1 s inx + cos x + sin 2 x + 5 = 0 ⇔ 2 sin x − 1 = 0 ⇔ s inx = 1 2 ⇔ x = π 6 k 2 π x = 5 π 6 + k 2 π
Với x ∈ 0 ; 3 π ⇒ x = π 6 ; 5 π 6 ; π 6 + 2 π ; 5 π 6 + 2 π ⇒ T = 6 π .

Đáp án D.
Phương trình tương với:
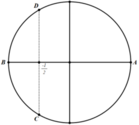
cos x − 2 cos 2 x − 1 − 4 cos 3 x − 3 cos x + 1 = 0 ⇔ − 4 cos 3 x − 2 cos 2 x + 4 cos x + 2 = 0 ⇔ 2 t 3 + t 2 − − 2 t − 1 = 0 t = cos x ⇔ t 2 − 1 2 t + 1 = 0 ⇔ t = 1 t = − 1 t = − 1 2
Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng − π ; 0 , phương trình có đúng 2 nghiệm (là − π và − 2 π 3 ).