Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Áp dụng bất đẳng thức Bunhiacopxki, ta có:
m . s inx+4cosx 2 ≤ m 2 + 4 2 sin 2 x + c os 2 x = m 2 + 16.
Nên để phương trình đã cho có nghiệm ⇔ 3 m − 5 2 ≤ m 2 + 16 ⇔ 3 m 2 20 m + 9 ≤ 0.
Kết hợp với m ∈ ℤ , ta được m = 1 ; 2 ; 3 ; 4 ; 5 ; 6 là giá trị cần tìm.

Đáp án D
Ta có: P T ⇔ 2 cos 2 x − 1 − 4 cos x = m
→ t − cos x f t = 2 t 2 − 4 t − 1 = m t ∈ − 1 ; 1
Khi đó: f ' t = 4 t − 4 = 0 ⇔ t = 1
Lại có: f 1 = 5 ; f 1 = − 3 do đó PT đã cho có nghiệm
⇔ m ∈ − 3 ; 5 ⇒ có 9 giá trị nguyên của m

Đáp án C
Ta có
cos 2 x − 4 cos x − m = 0 ⇔ 2 cos 2 x − 1 − 4 cos x − m = 0 ⇔ 2 cos 2 x − 4 cos x − 1 = m *
Đặt t = cos x ∈ − 1 ; 1 , khi đó * ⇔ m = f t = 2 t 2 − 4 t − 1 I .
Suy ra f t là hàm số nghịch biến trên − 1 ; 1 nên để I có nghiệm − 3 ≤ m ≤ 5
Vậy có tất cả 9 giá trị nguyên của tham số m cần tìm

Phương pháp:
- Đặt sinx = t, biến đổi điều kiện bài cho về điều kiện của phương trình ẩn t.
- Sử dụng bảng biến thiên để tìm điều kiện của m.
Cách giải:
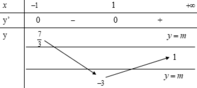
![]()
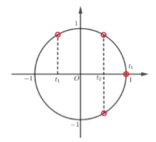
Phương trình đã cho có đúng 3 nghiệm phân biệt thuộc khoảng − π 2 ; π




![]()
![]()
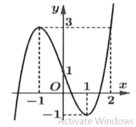
Do đó phương trình f[f(sinx)] = m có nghiệm thuộc khoảng 0 ; π khi và chỉ khi phương trình
f(t) = m có nghiệm thuộc nửa khoảng [-1;1]
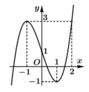
Dựa vào đồ thị, suy ra ![]()
Chọn C.
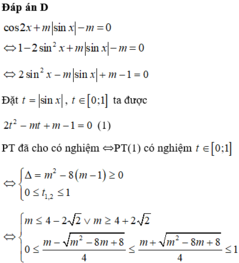
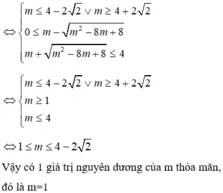





Chọn đáp án A.