S
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1
27 tháng 11 2018
\(\frac{y}{x\left(y-5x\right)}-\frac{15y-25x}{\left(y+5x\right)\cdot\left(y-5x\right)}\)
=\(\frac{y^2+5xy-15xy+25x^2}{x\left(y+5x\right)\left(y-5x\right)}\)
=\(\frac{y^2-10xy+25x^2}{x\left(y-5x\right)\left(y+5x\right)}=\frac{\left(y-5x\right)^2}{x\left(y-5x\right)\left(y+5x\right)}\)
=\(\frac{y-5x}{xy+5x^2}\)
4 tháng 12 2016
a)\(dk,x\ne7;x\ne0\)
\(\frac{4x+13}{5x\left(x-7\right)}-\frac{x-48}{5x\left(7-x\right)}=\frac{4x+13}{5x\left(x-7\right)}+\frac{x-48}{5x\left(x-7\right)}=\frac{\left(4x+13\right)+\left(x-48\right)}{5x\left(x-7\right)}\\ \)
\(=\frac{5x-35}{5x\left(x-7\right)}=\frac{5\left(x-7\right)}{5x\left(x-7\right)}=\frac{1}{x}\)
b)
\(\frac{1}{x-5x^2}-\frac{25x-15}{25x^2-1}=\frac{1}{x\left(1-5x\right)}+\frac{25x-15}{1-\left(5x\right)^2}=\frac{1}{x\left(1-5x\right)}+\frac{25x-15}{\left(1-5x\right)\left(1+5x\right)}\)
\(\frac{1+5x}{x\left(1-5x\right)\left(1+5x\right)}+\frac{x\left(25x-15\right)}{x\left(1-5x\right)\left(1+5x\right)}=\frac{25x^2-15x+5x+1}{x\left(1-5x\right)\left(1+5x\right)}=\frac{25x^2-10x+1}{x\left(1-5x\right)\left(1+5x\right)}\)
13 tháng 10 2019
a, \(ĐKXĐ:x\ne\pm\frac{1}{5},x\ne\frac{3}{2}\)
\(\Rightarrow P=\frac{\left(5x+1\right)\left(x+2\right)}{\left(2x-3\right)\left(5x-1\right)\left(5x+1\right)}-\frac{\left(8-3x\right)\left(5x+1\right)}{\left(5x-1\right)\left(5x+1\right)\left(2x-3\right)}\)
\(=\frac{x+2}{\left(2x-3\right)\left(5x-1\right)}-\frac{8-3x}{\left(5x-1\right)\left(2x-3\right)}\)
\(=\frac{2\left(2x-3\right)}{\left(2x-3\right)\left(5x-1\right)}=\frac{2}{5x-1}\)
b, Để P có giá trị nguyên thì \(2⋮5x-1\)
\(\Rightarrow5x-1\in\left\{1,2,-1,-2\right\}\)
=> x=..............
13 tháng 10 2019
ĐKXĐ : x \(\ne\frac{3}{2}\) ; \(x\ne\frac{1}{5};x\ne-\frac{1}{5}\)
P= \(\frac{5x+1}{2x-3}.\left(\frac{x+2}{25x^2-1}-\frac{8-3x}{25x^2-1}\right)\)
P= \(\frac{5x-1}{2x-3}.\left(\frac{4x-6}{\left(5x+1\right).\left(5x-1\right)}\right)\)
P= \(\frac{5x-1}{2x-3}.\frac{2\left(2x-3\right)}{\left(5x-1\right)\left(5x+1\right)}\)
P= \(\frac{2}{5x-1}\)
KL
2
16 tháng 12 2022
`a)1/[x-5x^2]-[25x-15]/[25x^2-1]`
`=[-(5x+1)-x(25x-15)]/[x(5x-1)(5x+1)]`
`=[-5x-1-25x^2+15x]/[x(5x-1)(5x+1)]`
`=[-25x^2+10x-1]/[x(5x-1)(5x+1)]`
`=[-(5x-1)^2]/[x(5x-1)(5x+1)]`
`=[1-5x]/[x(5x+1)]`
________________________________________________-
`b)(-1/[x^2-4x]+2/[16-x^2]-[-1]/[4x+16]):1/[4x]`
`=[-4(x+4)-8x+x(x-4)]/[4x(x-4)(x+4)].4x`
`=[-4x-16-8x+x^2-4x]/[(x-4)(x+4)]`
`=[x^2-16x-16]/[x^2-16]`
N
3
3 tháng 9 2020
\(\frac{y}{xy-5x^2}-\frac{15x-25x}{y^2-25x^2}\)
ĐKXĐ : \(\hept{\begin{cases}x,y\ne0\\y\ne\pm5x\end{cases}}\)
\(=\frac{y}{x\left(y-5x\right)}-\frac{-10x}{\left(y-5x\right)\left(y+5x\right)}\)
\(=\frac{y\left(y+5x\right)}{x\left(y-5x\right)\left(y+5x\right)}-\frac{-10xx}{x\left(y-5x\right)\left(y+5x\right)}\)
\(=\frac{y^2+5xy+10x^2}{x\left(y-5x\right)\left(y+5x\right)}\)
A
3 tháng 9 2020
\(\frac{y}{xy-5x^2}-\frac{-10x}{y^2-25x^2}=\frac{y^3-25x^2y}{\left(xy-5x^2\right)\left(y^2-25x^2\right)}-\frac{-10x^2y+50x^3}{\left(y^2-25x^2\right)\left(xy-5x^2\right)}\)
\(=\frac{y^3-25x^2y+10x^2y-50x^3}{\left(xy-5x^2\right)\left(y^2-25x^2\right)}=\frac{y^3-15x^2y-50x^3}{\left(xy-5x^2\right)\left(y^2-25x^2\right)}=\frac{y^3-50x^3}{x\left(y-5x\right)^2\left(y+5x\right)}\)
16 tháng 7 2015
???????????????????????????????????????????????????????????????????????????
TV
1
9 tháng 8 2016
\(\frac{6x-3}{5x^2+x}\cdot\frac{25x^2+10x+1}{1-8x^3}\)
\(=\frac{3\left(2x-1\right)}{x\left(5x+1\right)}\cdot\frac{\left(5x+1\right)^2}{\left(1-2x\right)\left(1+2x+4x^2\right)}\)
\(=-\frac{3\left(5x+1\right)}{x\left(1+2x+4x^2\right)}\)
9 tháng 8 2016
\(\frac{6x-3}{5x^2+x}.\frac{25x^2+10x+1}{1-8x^3}\)
\(=\frac{3\left(2x-1\right)\left(5x+1\right)^2}{x\left(5x+1\right)\left(1-2x\right)\left(1+2x+4x^2\right)}\)
\(=-\frac{3\left(5x+1\right)}{x\left(1+2x+4x^2\right)}\)
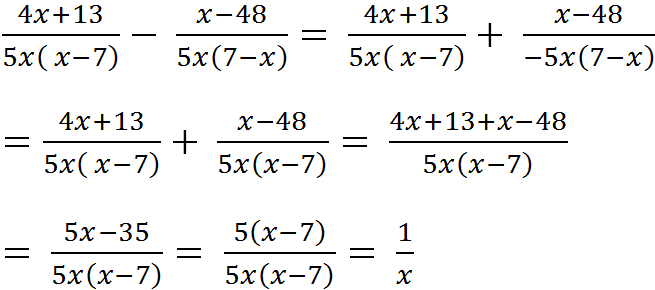
\(\frac{1}{x-5x^2}\)\(-\)\(\frac{25x-15}{25x^2-1}\)\(=\)\(\frac{-1}{x\left(5x-1\right)}\)\(-\)\(\frac{25x-15}{\left(5x-1\right)\left(5x+1\right)}\)
\(=\)\(\frac{-1\left(5x+1\right)}{x\left(5x-1\right)\left(5x+1\right)}\)\(-\)\(\frac{\left(25x^{ }-15\right)x}{\left(5x-1\right)\left(5x+1\right)x}\)
\(=\) \(\frac{-5x-1-25x^2+15x}{x\left(5x-1\right)\left(5x+1\right)}\)\(=\)\(\frac{-25x^2+10x-1}{x\left(5x-1\right)\left(5x+1\right)}\)
\(=\)\(\frac{-\left(5x-1\right)^2}{x\left(5x-1\right)\left(5x+1\right)}\)\(=\)\(\frac{-5x+1}{5x^2+x}\)
\(\frac{1}{x-5x^2}-\frac{25x-15}{25x^2-1}\)
\(=\frac{1}{x\left(1-5x\right)}-\frac{25x-15}{\left(5x-1\right)\left(5x+1\right)}\)
\(=\frac{1}{x\left(1-5x\right)}+\frac{25x-15}{\left(1-5x\right)\left(5x+1\right)}\)
\(=\frac{5x+1}{x\left(1-5x\right)\left(5x+1\right)}+\frac{\left(25x-15\right)x}{x\left(1-5x\right)\left(5x+1\right)}\)
\(=\frac{5x+1+25x^2+15x}{x\left(1-5x\right)\left(5x-1\right)}\)
\(=\frac{25x^2-10x+1}{x\left(1-5x\right)\left(5x+1\right)}\)
\(=\frac{\left(5x-1\right)^2}{x\left(1-5x\right)\left(5x+1\right)}\)
\(=\frac{\left(1-5x\right)^2}{x\left(1-5x\right)\left(5x+1\right)}\)
\(=\frac{1-5x}{x\left(5x+1\right)}\)