Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,đk:x\ne0;4;1\)
\(\dfrac{x-1}{x^2-5x+4}-\dfrac{4}{x^2-4x}\\ =\dfrac{x-1}{\left(x-1\right)\left(x-4\right)}-\dfrac{4}{x\left(x-4\right)}\\ =\dfrac{x\left(x-1\right)}{x\left(x-1\right)\left(x-4\right)}-\dfrac{4\left(x-1\right)}{x\left(x-1\right)\left(x-4\right)}\\ =\dfrac{x^2-x-4x+4}{x\left(x-1\right)\left(x-4\right)}\\ =\dfrac{x^2-5x+4}{x.\left(x-1\right)\left(x-4\right)}=\dfrac{\left(x-1\right)\left(x-4\right)}{x.\left(x-1\right)\left(x-4\right)}=\dfrac{1}{x}\)
\(đk:x\ne-2;1\)
\(\dfrac{x}{x+2}+\dfrac{7x-16}{\left(x+2\right)\left(7x-7\right)}\\ =\dfrac{x\left(7x-7\right)}{\left(x+2\right)\left(7x-7\right)}+\dfrac{7x-16}{\left(x+2\right)\left(7x-7\right)}\\ =\dfrac{7x^2-7x+7x-16}{\left(x+2\right)\left(7x-7\right)}\\ =\dfrac{7x^2-16}{\left(x+2\right)\left(7x-7\right)}\)
a)
\(\dfrac{x-1}{x^2-5x+4}-\dfrac{4}{x^2-4x}\) \(ĐKXĐ:x\ne0;x\ne4;x\ne1\)
\(=\dfrac{x-1}{x^2-4x-x+4}-\dfrac{4}{x\left(x-4\right)}\)
\(=\dfrac{x-1}{x\left(x-4\right)-\left(x-4\right)}-\dfrac{4}{x\left(x-4\right)}\)
\(=\dfrac{x-1}{\left(x-1\right)\left(x-4\right)}-\dfrac{4}{x\left(x-4\right)}\)
\(=\dfrac{x^2-x}{x\left(x-1\right)\left(x-4\right)}-\dfrac{4\left(x-1\right)}{x\left(x-1\right)\left(x-4\right)}\)
\(=\dfrac{x^2-x-4x+4}{x\left(x-1\right)\left(x-4\right)}\)
\(=\dfrac{x\left(x-1\right)-4\left(x-1\right)}{x\left(x-1\right)\left(x-4\right)}\)
\(=\dfrac{\left(x-1\right)\left(x-4\right)}{x\left(x-1\right)\left(x-4\right)}\\ =\dfrac{1}{x}\)
b)
\(\dfrac{x}{x+2}+\dfrac{7x-16}{\left(x+2\right)\left(7x-7\right)}\) \(ĐKXĐ:x\ne-2;x\ne1\)
\(=\dfrac{x\left(7x-7\right)}{\left(x+2\right)\left(7x-7\right)}+\dfrac{7x-16}{\left(x+2\right)\left(7x-7\right)}\)
\(=\dfrac{7x^2-7x+7x-16}{\left(x+2\right)\left(7x-7\right)}\)
\(=\dfrac{7x^2-16}{\left(x+2\right)\left(7x-7\right)}\)

a, \(\dfrac{4x+13}{5x\left(x-7\right)}-\dfrac{x-48}{5x\left(7-x\right)}\)
\(=\dfrac{4x+13}{5x\left(x-7\right)}+\dfrac{x-48}{5x\left(x-7\right)}\)
\(=\dfrac{4x+13+x-48}{5x\left(x-7\right)}\)
\(=\dfrac{5x-35}{5x\left(x-7\right)}\)
\(=\dfrac{5\left(x-7\right)}{5x\left(x-7\right)}=\dfrac{1}{x}\)
b, \(\dfrac{1}{x-5x^2}-\dfrac{25x-15}{25x^2-1}\)
\(=\dfrac{1}{x\left(1-5x\right)}+\dfrac{25x-15}{\left(1-5x\right)\left(1+5x\right)}\)
\(=\dfrac{1+5x}{x\left(x-5x\right)\left(1+5x\right)}+\dfrac{x\left(25x-15\right)}{x\left(1-5x\right)\left(1+5x\right)}\)
\(=\dfrac{1+5x+25x^2-15x}{x\left(1-5x\right)\left(1+5x\right)}\)\(=\dfrac{25x^2-10x+1}{x\left(1-5x\right)\left(1+5x\right)}=\dfrac{\left(5x-1\right)^2}{x.\left(1-5x\right)\left(1+5x\right)}\)
\(=\dfrac{\left(5x-1\right)^2}{-x\left(5x-1\right)\left(1+5x\right)}\) \(=\dfrac{-\left(5x-1\right)}{x\left(1+5x\right)}\)

b: \(=\dfrac{-1}{x\left(5x-1\right)}-\dfrac{25x-15}{\left(5x-1\right)\left(5x+1\right)}\)
\(=\dfrac{-5x-1-25x^2+15x}{x\left(5x-1\right)\left(5x+1\right)}\)
\(=\dfrac{-25x^2-10x-1}{x\left(5x-1\right)\left(5x+1\right)}=\dfrac{-\left(5x+1\right)}{x\left(5x-1\right)}\)
c: \(=\dfrac{x+9y}{\left(x-3y\right)\left(x+3y\right)}-\dfrac{3y}{x\left(x-3y\right)}\)
\(=\dfrac{x^2+9xy-3xy-9y^2}{x\left(x-3y\right)\left(x+3y\right)}\)
\(=\dfrac{x^2+6xy-9y^2}{x\left(x-3y\right)\left(x+3y\right)}\)
d: \(=\dfrac{3x+1}{\left(x-1\right)^2}-\dfrac{1}{x+1}+\dfrac{x+3}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{3x^2+4x+1-x^2+2x-1+x^2+2x-3}{\left(x-1\right)^2\cdot\left(x+1\right)}\)
\(=\dfrac{3x^2+8x-3}{\left(x-1\right)^2\cdot\left(x+1\right)}=\dfrac{3x^2+9x-x-3}{\left(x-1\right)^2\cdot\left(x+1\right)}\)
\(=\dfrac{3x+1}{\left(x-1\right)\left(x+1\right)}\)

a)\(\dfrac{x^2}{x-1}+\dfrac{1-2x}{x-1}\)
=\(\dfrac{x^2+1-2x}{x-1}\)
=\(\dfrac{x^2-2x+1}{x-1}\)
=\(\dfrac{\left(x-1\right)^2}{x-1}\)
= x - 1
b) \(\dfrac{x}{x-3}\) + \(\dfrac{-9}{x^2-3x}\)
=\(\dfrac{x}{x-3}\)+ \(\dfrac{-9}{x\left(x-3\right)}\)
=\(\dfrac{x.x}{x\left(x-3\right)}\) + \(\dfrac{-9}{x\left(x-3\right)}\)
=\(\dfrac{x^2+3^2}{x\left(x-3\right)}\)
=\(\dfrac{\left(x+3\right)\left(x-3\right)}{x\left(x-3\right)}\)
=\(\dfrac{x+3}{x}\)
#Fiona

a) \(=\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2}{x^2+x+1}-\dfrac{1}{x-1}=\dfrac{x^2+2+2\left(x-1\right)-\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+2+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)
b) \(=\dfrac{1}{x+2}+\dfrac{3}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-14}{\left(x+2\right)^2\left(x-2\right)}=\dfrac{\left(x+2\right)\left(x-2\right)+3\left(x+2\right)+x-14}{\left(x+2\right)^2\left(x-2\right)}=\dfrac{x^2-4+3x+6+x-14}{\left(x+2\right)^2\left(x-2\right)}=\dfrac{x^2+4x-12}{\left(x+2\right)^2\left(x-2\right)}=\dfrac{\left(x-2\right)\left(x+6\right)}{\left(x+2\right)^2\left(x-2\right)}=\dfrac{x+6}{\left(x+2\right)^2}\)
c) \(=\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{x^2-2xy+y^2+x^2-2xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{2\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)

ĐKXĐ: \(\left\{{}\begin{matrix}3x\ne-y\\3x\ne y\end{matrix}\right.\)
a. \(\dfrac{x}{3x+y}+\dfrac{x}{3x-y}-\dfrac{2xy}{y^2-9x^2}\)
\(=\dfrac{x.\left(3x-y\right)}{\left(3x+y\right).\left(3x-y\right)}+\dfrac{x.\left(3x+y\right)}{\left(3x+y\right).\left(3x-y\right)}+\dfrac{2xy}{9x^2-y^2}\)
\(=\dfrac{x.\left(3x+y+3x-y\right)+2xy}{\left(3x-y\right).\left(3x+y\right)}\)
\(=\dfrac{6x^2+2xy}{\left(3x-y\right).\left(3x+y\right)}\)
\(=\dfrac{2x\left(3x+y\right)}{\left(3x+y\right).\left(3x-y\right)}\)
\(=\dfrac{2x}{3x-y}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\x\ne-5\end{matrix}\right.\)
b. \(\dfrac{4x+5}{x^2+5x}-\dfrac{3}{x+5}\)
\(=\dfrac{4x+5}{x.\left(x+5\right)}-\dfrac{3x}{x.\left(x+5\right)}\)
\(=\dfrac{x+5}{x.\left(x+5\right)}\)
\(=\dfrac{1}{x}\)

a: \(=\dfrac{x+2y}{xy}\cdot\dfrac{2x^2}{\left(x+2y\right)^2}=\dfrac{2x}{y\left(x+2y\right)}\)
b: \(=\dfrac{x\left(4x^2-y^2\right)}{x^2+xy+y^2}\cdot\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(2x-y\right)^3}\)
\(=\dfrac{x\left(x-y\right)\left(2x+y\right)\left(2x-y\right)}{\left(2x-y\right)^3}\)
\(=\dfrac{x\left(x-y\right)\left(2x+y\right)}{\left(2x-y\right)^2}\)
c: \(=\dfrac{x+3}{x+2}\cdot\dfrac{2x-1}{3\left(x+3\right)}\cdot\dfrac{2\left(x+2\right)}{2\left(2x-1\right)}\)
=1/3
d: \(=\dfrac{x+1}{x+2}:\left(\dfrac{1}{2x}\cdot\dfrac{3x+3}{2x-3}\right)\)
\(=\dfrac{x+1}{x+2}\cdot\dfrac{2x\left(2x-3\right)}{3\left(x+1\right)}=\dfrac{2x\left(2x-3\right)}{3\left(x+2\right)}\)
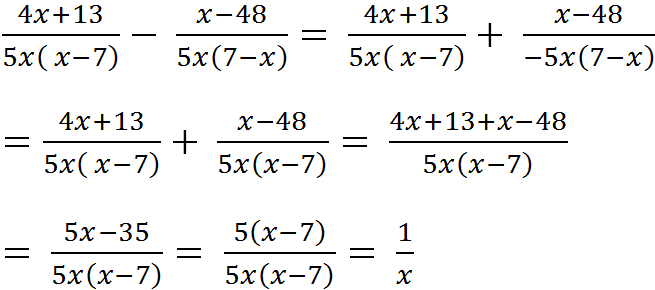

`a)1/[x-5x^2]-[25x-15]/[25x^2-1]`
`=[-(5x+1)-x(25x-15)]/[x(5x-1)(5x+1)]`
`=[-5x-1-25x^2+15x]/[x(5x-1)(5x+1)]`
`=[-25x^2+10x-1]/[x(5x-1)(5x+1)]`
`=[-(5x-1)^2]/[x(5x-1)(5x+1)]`
`=[1-5x]/[x(5x+1)]`
________________________________________________-
`b)(-1/[x^2-4x]+2/[16-x^2]-[-1]/[4x+16]):1/[4x]`
`=[-4(x+4)-8x+x(x-4)]/[4x(x-4)(x+4)].4x`
`=[-4x-16-8x+x^2-4x]/[(x-4)(x+4)]`
`=[x^2-16x-16]/[x^2-16]`