
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(x=a;2y=b;z=c\)
\(A=\left(a+b-c\right)^3-a^3-b^3+c^3\)
\(A=\left[a+\left(b-c\right)\right]^3-a^3-b^3+c^3\)
\(A=a^3+3a\left(b-c\right)\left(a+b-c\right)+\left(b-c\right)^3-a^3-b^3+c^3\)
\(A=a^3-3a\left(b-c\right)\left(a+b-c\right)+b^3+3bc\left(b-c\right)-c^3-a^3-b^3+c^3\)
\(A=3\left(b-c\right)\left(a^2+ab-ac+bc\right)\)
\(A=3\left(b-c\right)\left(a+b\right)\left(a-c\right)\)
Khi đó ta có:
\(A=3\left(x-z\right)\left(x+2y\right)\left(2y-z\right)\)

Đặt \(x+y-z=a;x-y+z=b;y+z-x=c\)
Ta có:\(A=\left(a+b+c\right)^3-a^3-b^3-c^3\)
\(A=\left[\left(a+b\right)+c\right]^3-a^3-b^3-c^3\)
\(A=\left(a+b\right)^3+3\left(a+b\right)\cdot c\cdot\left(a+b+c\right)+c^3-a^3-b^3-c^3\)
\(A=a^3+b^3+3ab\left(a+b\right)+3\left(a+b\right)c\left(a+b+c\right)+c^3-a^3-b^3-c^3\)
\(A=3\left(a+b\right)\left(ab+ac+bc+c^2\right)\)
\(A=3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Hay \(A=3\cdot2x\cdot2y\cdot2z\)
\(A=24xyz\)

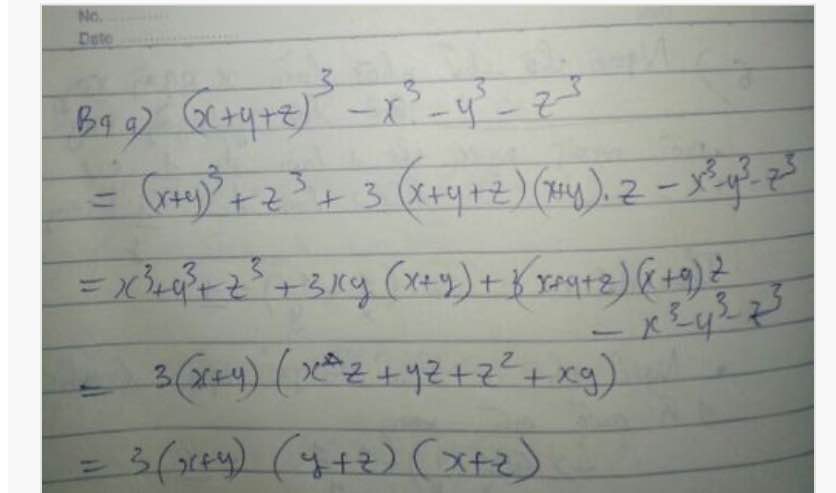
Bạn tham khảo tại đây:
Câu hỏi của Nguyễn Công Minh Hoàng - Toán lớp 8 - Học toán với OnlineMath