K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 3 2018
\(\left(x^3-2x^2\right)-\left(4x^2-8x\right)+\left(x-2\right).\)
\(x^2\left(x-2\right)-4x\left(x-2\right)+\left(x-2\right)\)
vậy................
2 tháng 3 2018
\(\left(x^3-2x^2\right)-\left(4x^2-8x\right)+\left(x-2\right)\)
\(x^2\left(x-2\right)-4x\left(x-2\right)+\left(x-2\right)\)
Vậy ........
24 tháng 7 2021
Ta có: \(4x^2+12x+9\)
\(=4x^2+6x+6x+9\)
\(=2x\left(2x+3\right)+3\left(2x+3\right)\)
\(=\left(2x+3\right)^2\)
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Lời giải:
$x^4y^4-z^4=(x^2y^2)^2-(z^2)^2=(x^2y^2-z^2)(x^2y^2+z^2)$
$=(xy-z)(xy+z)(x^2y^2+z^2)$
$(x+y+z)^2-4z^2=(x+y+z)^2-(2z)^2=(x+y+z-2z)(x+y+z+2z)$
$=(x+y-z)(x+y+3z)$
$\frac{-1}{9}x^2+\frac{1}{3}xy-\frac{1}{4}y^2=\frac{-4x^2+12xy-9y^2}{36}$
$=-\frac{4x^2-12xy+9y^2}{36}=-\frac{(2x-3y)^2}{36}=-\left(\frac{2x-3y}{6}\right)^2$
5 tháng 6 2016
\(x^2+x-6=x^2-2x+3x-6=x\left(x-2\right)+3\left(x-2\right)=\left(x-2\right)\left(x+3\right)\)
5 tháng 6 2016
x2 + x - 6
= x2 - 2x + 3x - 6
= x ( x - 2 ) + 3 ( x - 2 )
= ( x - 2 ) ( x + 3 )
TN
2
LC
31 tháng 7 2016
=m^3-3m^2-3m^2+9n+2m-6
=m^2(m-3)-3m(m3)+2(m-3)
=(m-3)(m^2-3m+2)=(m-3)(m^2-m-2m+2)
=(m-3)[m(m-1)-2(m-1)]
=(m-3)(m-2)(m-1)
31 tháng 7 2016
\(m^3-6m^2+11m-6\)
\(m^3-6m^2+11m-6\)
\(=\left(m-1\right)\left(m-3\right)\left(m-2\right)\)
31 tháng 7 2021
19) Ta có: \(-x^2-4x-4\)
\(=-\left(x^2+4x+4\right)\)
\(=-\left(x+2\right)^2\)
20) Ta có: \(-4x^2-12x-9\)
\(=-\left(4x^2+12x+9\right)\)
\(=-\left(2x+3\right)^2\)
21) Ta có: \(-4x^2-4x-1\)
\(=-\left(4x^2+4x+1\right)\)
\(=-\left(2x+1\right)^2\)
22) Ta có: \(-x^2+6x-9\)
\(=-\left(x^2-6x+9\right)\)
\(=-\left(x-3\right)^2\)
23) Ta có: \(-x^2+10x-25\)
\(=-\left(x^2-10x+25\right)\)
\(=-\left(x-5\right)^2\)
24) Ta có: \(-x^2+8x-16\)
\(=-\left(x^2-8x+16\right)\)
\(=-\left(x-4\right)^2\)
25) Ta có: \(-4x^2+12x-9\)
\(=-\left(4x^2-12x+9\right)\)
\(=-\left(2x-3\right)^2\)
26) Ta có: \(a^2-a+b-b^2\)
\(=\left(a-b\right)\left(a+b\right)-\left(a-b\right)\)
\(=\left(a-b\right)\left(a+b-1\right)\)
31 tháng 7 2021
13) Ta có: \(y^2-2xy+2x-y\)
\(=y\left(y-2x\right)-\left(y-2x\right)\)
\(=\left(y-2x\right)\left(y-1\right)\)
14) Ta có: \(x-2xy+4y-2\)
\(=x\left(1-2y\right)-2\left(1-2y\right)\)
\(=\left(1-2y\right)\left(x-2\right)\)
15) Ta có: \(x^2-2xy+x-2y\)
\(=x\left(x-2y\right)+\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x+1\right)\)
16) Ta có: \(xy-z-y+xz\)
\(=x\left(y+z\right)-\left(y+z\right)\)
\(=\left(y+z\right)\left(x-1\right)\)
17) Ta có: \(2xy+3z-6y-xz\)
\(=\left(2xy-xz\right)+\left(3z-6y\right)\)
\(=x\left(2y-z\right)-3\left(2y-z\right)\)
\(=\left(2y-z\right)\left(x-3\right)\)
18) Ta có: \(2xy-2z+4y-xz\)
\(=\left(2xy+4y\right)+\left(xz+2z\right)\)
\(=2y\left(x+2\right)+z\left(x+2\right)\)
\(=\left(x+2\right)\left(2y+z\right)\)
8 tháng 8 2021
26) Ta có: \(x^4-20x^2+64\)
\(=x^4-16x^2-4x^2+64\)
\(=x^2\left(x^2-16\right)-4\left(x^2-16\right)\)
\(=\left(x-4\right)\left(x+4\right)\left(x-2\right)\left(x+2\right)\)
27) Ta có: \(4x^3+6x^2+3x+1\)
\(=4x^3+4x^2+2x^2+2x+x+1\)
\(=4x^2\left(x+1\right)+2x\left(x+1\right)+\left(x+1\right)\)
\(=\left(x+1\right)\left(4x^2+2x+1\right)\)
28) Ta có: \(x^3-6x^2+12x-9\)
\(=x^3-3x^2-3x^2+9x+3x-9\)
\(=x^2\cdot\left(x-3\right)-3x\left(x-3\right)+3\left(x-3\right)\)
\(=\left(x-3\right)\left(x^2-3x+3\right)\)
29: Ta có: \(x^4+x^2+1\)
\(=x^4+2x^2+1-x^2\)
\(=\left(x^2+1\right)^2-x^2\)
\(=\left(x^2-x+1\right)\left(x^2+x+1\right)\)
HN
9 tháng 8 2021
26) Ta có: x4−20x2+64x4−20x2+64
=x4−16x2−4x2+64=x4−16x2−4x2+64
=x2(x2−16)−4(x2−16)=x2(x2−16)−4(x2−16)
=(x−4)(x+4)(x−2)(x+2)=(x−4)(x+4)(x−2)(x+2)
27) Ta có: 4x3+6x2+3x+14x3+6x2+3x+1
=4x3+4x2+2x2+2x+x+1=4x3+4x2+2x2+2x+x+1
=4x2(x+1)+2x(x+1)+(x+1)=4x2(x+1)+2x(x+1)+(x+1)
=(x+1)(4x2+2x+1)=(x+1)(4x2+2x+1)
28) Ta có: x3−6x2+12x−9x3−6x2+12x−9
=x3−3x2−3x2+9x+3x−9=x3−3x2−3x2+9x+3x−9
=x2⋅(x−3)−3x(x−3)+3(x−3)=x2⋅(x−3)−3x(x−3)+3(x−3)
=(x−3)(x2−3x+3)=(x−3)(x2−3x+3)
29: Ta có: x4+x2+1x4+x2+1
=x4+2x2+1−x2=x4+2x2+1−x2
=(x2+1)2−x2=(x2+1)2−x2
=(x2−x+1)(x2+x+1)
NT
2
5 tháng 7 2017
a) \(x^4-y^4=\left(x^2\right)^2-\left(y^2\right)^2=\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x+y\right)\left(x-y\right)\left(x^2+y^2\right)\)
c) \(36-12x+x^2=x^2-12x+36=x^2-6x-6x+36\)
\(=x\left(x-6\right)-6\left(x-6\right)=\left(x-6\right)\left(x-6\right)=\left(x-6\right)^2\)
5 tháng 7 2017
\(x^4-y^4\)
\(=\left(x^2-y^2\right)\left(x^2+y^2\right)\)
\(=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
\(4x^2+12x+9\)
\(=\left(2x\right)^2+2.2x.3+9\)
\(=\left(2x+3\right)^2\)
\(36-12x+x^2\)
\(=6^2-2.6.x+x^2\)
\(=\left(6-x\right)^2\)
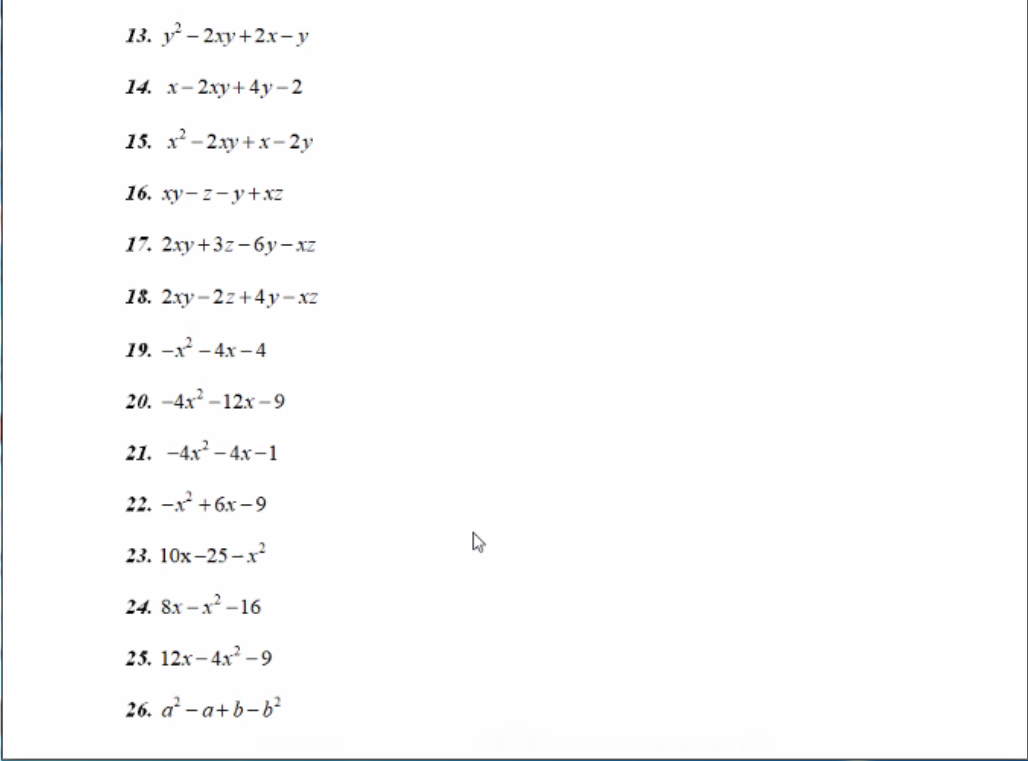
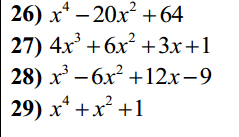
(x^3-3x-3)(x^6+3x^4-6x^3+9x^2-9x+9)