Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
z 2 − z + 1 = 0 ⇔ z 1 , 2 = 1 ± 3 i 2 ⇒ z = 1 + 3 i 2 ⇒ a = 1 2 , b = 3 2 ⇒ a + 3 b = 2

Đáp án A
Phương trình z 2 − z + 2017 2 = 0 ⇔ 4 z 2 − 4 z + 2017 = 0
⇔ 2 z − 1 2 = 2016 i 2 ⇔ z 1 = 1 − i 2016 2 z 2 = 1 + i 2016 2
Ta có z − z 1 + z − z 2 ≥ z − z 1 − z − z 2 = z − z 2 ≥ z 1 − z 2 − z − z 1 = 2016 − 1
Vật giá trị nhỏ nhất của biểu thức P là P min = 2016 − 1

Từ giả thiết suy ra z 1 ; z 2 không phải là số thực. Khi đó
∆ ' < 0 ⇔ a + 1 2 - 8 4 a + 1 ⇔ 4 a 2 - 6 a - 1 < 0
Suy ra
z 1 = a + 1 - - a 2 - 6 a + 1 t 2 4 z 2 = a + 1 - a 2 - 6 a + 1 t 2 4
z 1 z 2 là số ảo z 1 2 là số ảo
⇔ a + 1 2 - - a 2 - 6 a - 1 ⇔ a 2 - 2 a = 0 ⇔ a = 0 a = 2
Thay vào điều kiện (*) thấy thỏa mãn.
Đáp án C




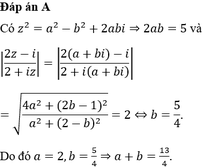


Đáp án A
Phương pháp :
Tìm nghiệm phức có phần ảo dương của phương trình z2 – z +1 = 0 bằng MTCT.
Cách giải:
Sử dụng MTCT ta tính được nghiệm phức có phần ảo dương của phương trình trên là