Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Gọi M(1;0) thuộc (d)
Theo đề, ta có: \(\overrightarrow{IM'}=k\cdot\overrightarrow{IM}\)
=>\(\left\{{}\begin{matrix}x_{M'}-1=k\cdot\left(1-1\right)=0\\y_{M'}=k\cdot\left(0-0\right)=0\end{matrix}\right.\)
=>M'(1;0)
Thay M' vào x+2y+c=0, ta được:
1+c=0
=>c=-1

Đáp án C
Những phát biểuđúng: 1; 4; 5; 6; 7; 8; 9; 10; 11; 13; 14
2. Qua phép vị tự có tỉ số , đường tròn có tâm là tâm vị tự sẽ biến thành 1 đường tròn đồng tâm với đường tròn ban đầu và có bán kính = k. bán kính đường tròn ban đầu.
3. Qua phép vị tự có tỉ số đường tròn biến thành chính nó.
12. Phép vị tự với tỉ số k = biến tứ giác thành tứ giác bằng nó

Phương trình đường thẳng d: x - y - 1= 0
Lấy M(x; y) thuộc d
Phép vị tự tâm O(0; 0) tỉ số k = 3 biến điểm M thành M’(x’; y’) thì O M ' → = 3 O M → ⇔ x ' = 3 x y ' = 3 y ⇔ x = 1 3 x ' y = 1 3 y '
Phép đối xứng trục Ox biến M’(x’; y’) thành M’’(x’’; y’’)
Thay vào phương trình d ta được: ⇔ x ' ' = x ' y ' ' = − y ' ⇔ x = 1 3 x ' ' y = − 1 3 y ' '
Hay x’’ + y’’ - 3 = 0
Vậy phương trình đường thẳng d’: x + y - 3 = 0.
Đáp án B

Câu 1:
Theo đề, ta có: \(\overrightarrow{IM'}=-2\cdot\overrightarrow{IM}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=-2\cdot\left(-7-2\right)=18\\y-3=-2\cdot\left(2-3\right)=2\end{matrix}\right.\Leftrightarrow M'\left(20;5\right)\)

Với cái đề này thì cho phép mình xin tạm hiểu là phép \(V_{\left(I;2\right)}\left(A\right)=A'\) và B' là ảnh của A' qua phép đối xứng tâm B nha
Tọa độ A' là:
\(\overrightarrow{IA'}=2\cdot\overrightarrow{IA}\)
=>\(\left\{{}\begin{matrix}x_{A'}-2=2\cdot\left(1-2\right)=-2\\y_{A'}+1=2\left(1+1\right)=4\end{matrix}\right.\Leftrightarrow A'\left(0;3\right)\)
Theo đề, ta có: \(\left\{{}\begin{matrix}x_B=\dfrac{x_{A'}+x_{B'}}{2}\\y_B=\dfrac{y_{A'}+y_{B'}}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_{B'}+0=2\cdot\left(-3\right)=-6\\y_{B'}+3=2\cdot1=2\end{matrix}\right.\Leftrightarrow B'\left(-6;-1\right)\)

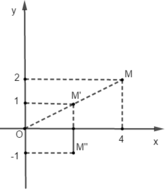
V ( 0 ; 1 / 2 ) ( M ( 4 ; 2 ) ) = M ' ( 2 ; 1 ) ; Đ O x ( M ' ( 2 ; 1 ) ) = M " ( 2 ; - 1 ) .
Đáp án A.
Bài 1:
\(AB=\sqrt{\left(4+2\right)^2+\left(1+3\right)^2}=\sqrt{6^2+4^2}=2\sqrt{13}\)
\(A'B'=\dfrac{1}{2}\cdot AB=\dfrac{1}{2}\cdot2\sqrt{13}=\sqrt{13}\)