Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi t là thời gian xe đi hết quãng đường s
v=v0-a.t\(\Rightarrow\)v0=a.t
quãng đường đi với t thời gian là
s=v0.t-a.t2.0,5=a.t2-a.t2.0,5=0,5.a.t2
quãng đường đi được trong 2 giây đầu
s1=\(v_0.t_2-a.t_2^2.0,5\)\(\Rightarrow s_1=2at-2a\)
quãng đường đi được với t-2 giây đầu
s2=v0(t-2)-a.(t-2)2.0,5=\(0,5.t^2.a-2a\)
theo đề bài ta có
s2-s1=160m\(\Leftrightarrow0,5.t^2.a-2at\)=160 (1)
quãng đường đi được trong 2 giây cuối
s3=s-s2=2a
theo đề bài ta có
s1-s3=36m\(\Rightarrow\)2at-4a=36 (2)
từ (1),(2) giải hệ phương trình ta được
t=20s
vậy thời gian chuyển động chậm dần đến khi dừng lại là 20s

1) \(v^2-v_0^2=2as\)
=> \(5^2-v_0^2=2a.10\)
=> \(25-v_0^2=20a\) (1)
lại có: \(10^2-v_0^2=2a.47,5\)
=> \(100-v^2_0=95a\) (2)
từ (1) và (2) ta có hệ : \(\left\{{}\begin{matrix}25-v_0^2=20a\\100-v_0^2=95a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=1m/s^2\\v_0=\sqrt{5}m/s\end{matrix}\right.\)

Bài 1
Tóm tắt: \(v_A=6\left(\dfrac{m}{s}\right);\\ v_B=8\left(\dfrac{m}{s}\right);\\ s_{AC}=s_{CB}\\ v_{tb}=?\)
Giải:
-Vận tốc trung bình là
ADCT: \(v_{tb}=\dfrac{1}{\dfrac{1}{2}\left(\dfrac{1}{v_A}+\dfrac{1}{v_B}\right)}=\dfrac{1}{\dfrac{1}{2}\left(\dfrac{1}{6}+\dfrac{1}{8}\right)}=\dfrac{48}{7}\approx6,86\left(\dfrac{m}{s}\right)\)

Quãng đường đi được trong 1s cuối
\(\dfrac{1}{2}\cdot a\cdot5^2-\dfrac{1}{2}\cdot a\cdot\left(5-1\right)^2=1,5\Rightarrow a=\dfrac{1}{3}\left(\dfrac{m}{s^2}\right)\)
Vậy gia tốc của vật là 1/3 (m/s^2)
Quãng đường đi dc từ khi hãm phanh đến khi dừng lại
\(s=\dfrac{1}{2}\cdot\dfrac{1}{3}\cdot5^2=\dfrac{25}{6}\left(m\right)\)
<chỗ nào sai chỉ mình hoặc ko hiểu thì bình luận câu trả lời nha>
\(v^2-v^2_0=2as\)
\(\Rightarrow5^2-v^2_0=2a.10\)
\(\Rightarrow25-v^2_0=20a\left(1\right)\)
Lại có: \(10^2-v^2_0=2a.47,5\)
\(\Rightarrow100-^2_0=95a\left(2\right)\)
Từ (1) và (2) ta có hệ : \(\left\{{}\begin{matrix}25-v^2_0=20a\\100-v^2_0=95a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=1m\text{/ }s^2\\v_0=\sqrt{5m\text{/ }s}\end{matrix}\right.\)

1)
v0=0
Sgiây thứ 3 = 5m \(\Leftrightarrow S_{giâythứ3}=v_0t+\frac{1}{2}at^2-v_0\left(t-1\right)-\frac{1}{2}a\left(t-1\right)^2=v_0+a\left(t-\frac{1}{2}\right)=0+a\left(3-\frac{1}{2}\right)=\frac{5}{2}a\)
=> \(\frac{5}{2}a=5\)
=> a =2\(m/s^2\)
Quãng đường xe đi được sau 10s là:
t =10s => \(s=v_0t+\frac{1}{2}at^2=\frac{1}{2}.2.10^2=100\left(m\right)\)
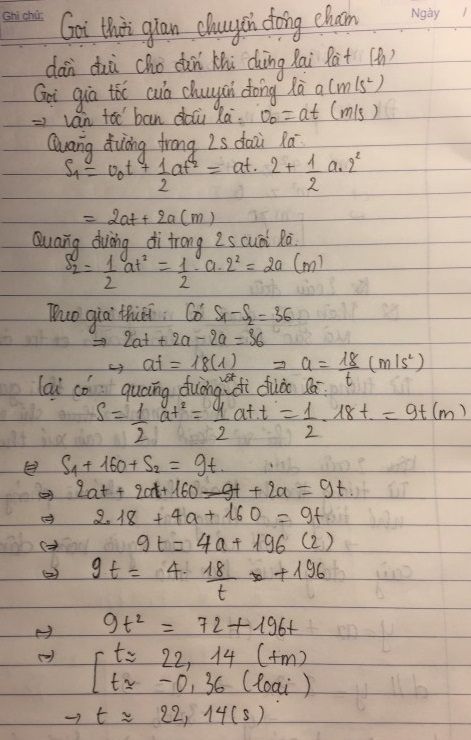
Những bài toán như thế này thuộc kiểu bài toán giải bằng cách lập phương trình, hệ phương trình.
Gọi thời gian chuyển động chậm dần đều cho đến khi dừng lại là $t$
Gọi gia tốc của chuyển động là $a$
Suy ra vận tốc ban đầu là: $v_0=a.t$
Quãng đường trong 2s đầu là:
\(S_1=v_0t+\dfrac{1}{2}at^2=at.2+\dfrac{1}{2}a.2^2=2at+2a\)
Quãng đường đi trong 2s cuối là:
\(S_2=\dfrac{1}{2}at^2=\dfrac{1}{2}.a.2^2=2a\) (vì cuối cùng vật dừng lại nên ta áp dụng công thức ngược)
Theo giả thiết ta có: \(S_1-S_2=36\)
\(\Rightarrow 2at+2a-2a=36\)
\(\Rightarrow at =18\) (1)
Tổng quãng đường vật đã đi là: \(S=\dfrac{1}{2}at^2=\dfrac{1}{2}.at.t=\dfrac{1}{2}.18.t=9t\)
Theo giả thiết ta có: \(S=S_1+160+S_2\)
\(\Rightarrow 9t=2at+2a+160+2a\)
\(\Rightarrow 9t=2.18+4a+160\)
\(\Rightarrow 9t=4a+196\) (2)
Từ (1) suy ra \(a=\dfrac{18}{t}\), thay vào (2) ta được:
\(9t=\dfrac{4.18}{t}+196\)
\(\Rightarrow 9t^2-196t-72=0\)
\(\Rightarrow t \approx 22,14s\)
Cảm ơn bạn rất nhiều. Mình chưa hiểu lắm. Mình nghiên cứu thêm đã rồi báo lại bạn sau.