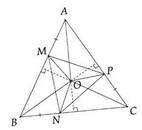
a, Vì \(\Delta ABC\) đều và \(O\) là giao điểm 3 đường trung trực nên \(AO\) là tia phân giác của \(\widehat{A}\)

\(\Rightarrow\widehat{MAO}=\dfrac{\widehat{BAC}}{2}=30^o\)

b, Tương tự a, \(\widehat{OCB}=30^o\)

Chứng minh được: \(\Delta MAO=\Delta OPC\left(c.g.c\right)\)

Ta có: \(\Delta MAO=\Delta OPC\Rightarrow OM=OP\left(1\right)\)

c, Tương tự b

\(\Delta MAO=\Delta NBO\left(c.g.c\right)\)

\(\Rightarrow ON=OM\left(2\right)\)

Từ (1) và (2) suy ra O là giao điểm

3 đương trung trực của tam giác MNP

Câu 2:

- Có 2 nhân vật: là Dế Mèn và hai con chim Én

- Chi tiết miêu tả hành động:

+ Dế Mèn: thơ thẩn ở cửa hang, bay, ngậm vào giữa, chợt nghĩ, há mồm ra, rơi vèo 

+ Chim Én: ngậm đầu, bay lên

Chiều dài của đất đó là: 

    \(12768\times2=25536\) ( đơn vị )

Chu vi của đất đó là: 

     \(\left(25536+12768\right)\times2=76608\) ( đơn vị )

Câu 21: B. Don't

Câu 22: D. cartoon

Câu 23: C. might 

Câu 24: C. If

Câu 25: A. because

Câu 26: D. next

Câu 27: A. sport

Câu 28: A. outdoor

Câu 29: C. sporty

Câu 30: A. hot

Câu 31: C. during

\(\dfrac{1}{2}\times\dfrac{3}{4}+\dfrac{1}{2}\times\dfrac{1}{4}+\dfrac{1}{2}\)

\(=\dfrac{1}{2}\times\left(\dfrac{3}{4}+\dfrac{1}{2}\right)\times\dfrac{1}{4}\)

\(=\dfrac{1}{2}\times\dfrac{5}{4}\times\dfrac{1}{4}\)

\(=\dfrac{5}{32}\)

\(\left(\dfrac{1}{2}+\dfrac{1}{3}\right)\times\dfrac{5}{6}\)

\(=\left(\dfrac{3}{6}+\dfrac{2}{6}\right)\times\dfrac{5}{6}\)

\(=\dfrac{5}{6}\times\dfrac{5}{6}\)

\(=\dfrac{10}{12}\)