Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
+ Hai dao động vuông pha: ![]()
+ Gia tốc cực đại: amax = ω2A = 102.0,075 = 7,5 m/s2.

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

\(x_1 = 5 \cos (\omega t + \varphi)cm.\)
\(x_2 = A_2 \cos (\omega t - \frac{\pi}{4})cm.\)
\(x= A \cos (\omega t - \frac{\pi}{12})cm.\)
Vẽ giản đồ véc tơ như hình vẽ
Áp dụng định lý hàm số Sin ta có:
Xét: \(\triangle OA_1A:\) \(\frac{A}{\sin OA_1A} = \frac{A_1}{\sin OAA_1} \)
=> \(\frac{A}{\sin (\frac{3\pi}{4}-\varphi)} = \frac{A_1}{\sin (\frac{\pi}{6})} \)
=> \(A= \frac{A_1}{\sin (\frac{\pi}{6})} .\sin (\frac{3\pi}{4}-\varphi).(*)\)
TH1: \(A= A _{max} <=> \sin (\frac{3\pi}{4}-\varphi) = 1\)
=> \(A_{max}= \frac{A_1}{\sin (\frac{\pi}{6})}= 10cm.(1)\)
TH2: \(A = \frac{A_{max}}{2} => \sin (\frac{3\pi}{4}-\varphi) = \frac{1}{2}.\)
=> \(\frac{3\pi}{4} - \varphi = \frac{\pi}{6}\)
=> \(\varphi = \frac{7\pi}{12}.(2)\)
Xét: \(\triangle OA_2A:\) \(\frac{A}{\sin OA_2A} = \frac{A_2}{\sin OAA_2} \)
=> \(\frac{A}{\sin (\frac{3\pi}{4}-\varphi)} = \frac{A_2}{\sin (\varphi+\frac{\pi}{12})} \)
=> \(A_2= \frac{A_{max}}{\sin (\frac{3\pi}{4}-\varphi)} .\sin (\frac{\pi}{12}+\varphi).(3)\)
Thay \((1); (2)\) vào \((3)\) ta được: \(A_2= \frac{10}{0,5} .\sin (\frac{\pi}{12}+\frac{7\pi}{12}) = \frac{10}{0,5}.\frac{\sqrt{3}}{2} = 10 \sqrt{3}cm.\)
Chọn đáp án.C.\(10\sqrt{3}cm.\)
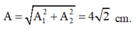
pi / 3