Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
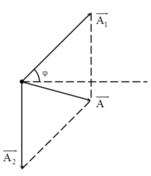
Từ hình vẽ, áp dụng định lý hàm cos trong tam giác ta có:
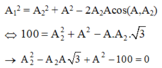
Phương trình trên luôn có nghiệm nên:


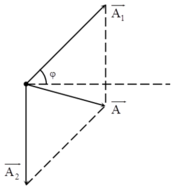
- Từ hình vẽ, áp dụng định lý hàm cos trong tam giác ta có:
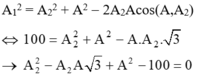
- Phương trình trên luôn có nghiệm nên:
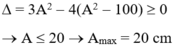
- Với: 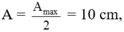
thay vào phương trình trên ta được: 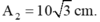


![]()
![]()
Bình luận: Để nhanh chóng tìm được kết quả ta chuẩn hóa nhanh như sau
*Lập tỉ giữa 2 trong 3 phương trình trên ta được:
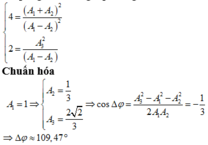

+ Ta có
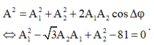
Để phương trình trên tồn tại nghiệm A 1 thì
![]()
Thay giá trị A 2 vào phương trình đầu, ta tìm được
![]()
Đáp an A


\(\overrightarrow{A}=\overrightarrow{A_1}+\overrightarrow{A_2}\)
Định lý hàm sin: \(\dfrac{A}{\sin\dfrac{\pi}{6}}=\dfrac{A_2}{\sin\alpha}=\dfrac{A_1}{\sin\beta}\)
\(A_2\left(max\right)\Rightarrow\sin\alpha_{max}=1\Rightarrow\left\{{}\begin{matrix}A_2=\dfrac{9}{\dfrac{1}{2}}=18\left(cm\right)\\\alpha=\dfrac{\pi}{2}\left(rad\right)\end{matrix}\right.\)
\(\Rightarrow\beta=\pi-\dfrac{\pi}{6}-\dfrac{\pi}{2}=\dfrac{\pi}{3}\left(rad\right)\Rightarrow A_1=18.\sin\dfrac{\pi}{3}=9\sqrt{3}\left(cm\right)\)

Đáp án D

Theo định lý hàm sin: A sin α = 5 sin 30 ⇒ A = 10 sin α
Giá trị max của A = 10 c m nếu sin α = 1 . Đề bài yêu cầu A bằng 1 nửa giá trị này, tức là sin α = 0 , 5 . Lúc đó α = 30 ° .
Áp dụng định lý hàm cosin cho tam giác:
A 2 2 = 5 2 + 5 2 − 2.5.5. c os 120 ⇒ A 2 = 5 3 ( c m )

Đáp án D
+ Ta có:
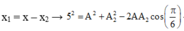
![]()
→ Để phương trình có nghiệm A2 thì ∆ = 3 A 2 - 4 ( A 2 - 25 ) ≥ 0 → A m a x = 10 cm
→ Với A = 0,5Amax = 5 cm → A 2 = 5 3 c m
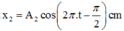
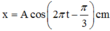
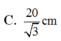
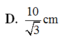


Giải thích: Đáp án B
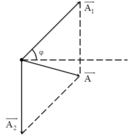
Phương pháp: Sử dụng giản đồ vecto
Cách giải:
- Từ dữ kiện đề bài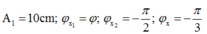 ta vẽ được giản đồ vecto:
ta vẽ được giản đồ vecto:
- Xét ∆OA2A ta có: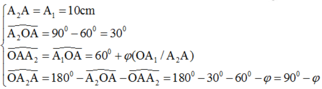
- Sử dụng định lí hàm số sin trong ∆OA2A ta có: