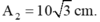Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Từ hình vẽ, áp dụng định lý hàm cos trong tam giác ta có:
Phương trình trên luôn có nghiệm nên:


Hướng dẫn: Chọn đáp án B
Cách 1:
![]()
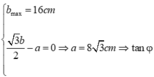
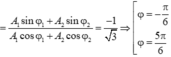
Cách 2: Áp dụng định lý hàm số sin ta có
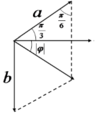
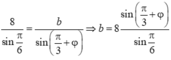
b đạt cực đại khi
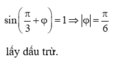

+ Ta có
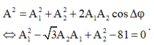
Để phương trình trên tồn tại nghiệm A 1 thì
![]()
Thay giá trị A 2 vào phương trình đầu, ta tìm được
![]()
Đáp an A


\(\overrightarrow{A}=\overrightarrow{A_1}+\overrightarrow{A_2}\)
Định lý hàm sin: \(\dfrac{A}{\sin\dfrac{\pi}{6}}=\dfrac{A_2}{\sin\alpha}=\dfrac{A_1}{\sin\beta}\)
\(A_2\left(max\right)\Rightarrow\sin\alpha_{max}=1\Rightarrow\left\{{}\begin{matrix}A_2=\dfrac{9}{\dfrac{1}{2}}=18\left(cm\right)\\\alpha=\dfrac{\pi}{2}\left(rad\right)\end{matrix}\right.\)
\(\Rightarrow\beta=\pi-\dfrac{\pi}{6}-\dfrac{\pi}{2}=\dfrac{\pi}{3}\left(rad\right)\Rightarrow A_1=18.\sin\dfrac{\pi}{3}=9\sqrt{3}\left(cm\right)\)

Chọn đáp án C
A t 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos φ ⇔ 20 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos 11 18 π
⇒ 20 2 = A 1 + A 2 2 − 2 , 68. A 1 A 2 ≥ A 1 + A 2 2 − 2 , 68. A 1 + A 2 2 4 = 0 , 33 A 1 + A 2 2
⇒ A 1 + A 2 ≤ 34 , 9 c m .

Đáp án D
Ta nhận thấy x1 và x3 ngược pha nhau và cùng vuông pha với x2 nên khi x2 cực tiểu thì x1;x3 cực đại
![]()
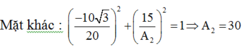
Biên độ dao động tổng hợp :
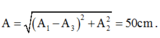

- Ta nhận thấy x1 và x3 ngược pha nhau và cùng vuông pha với x2 nên khi x2 cực tiểu thì x1; x3 cực đại:
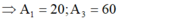
- Mặt khác:
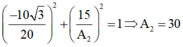
- Biên độ dao động tổng hợp:
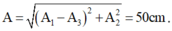
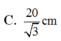
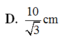
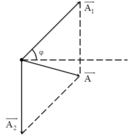

- Từ hình vẽ, áp dụng định lý hàm cos trong tam giác ta có:
- Phương trình trên luôn có nghiệm nên:
- Với: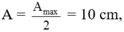
thay vào phương trình trên ta được: