Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi x là số sản phẩm làm 1 ngày theo dự định
3200/x là số ngày làm 3200 sp theo dự định
5+(3200-5x)/(x+40) là số ngày làm xong sản phẩm thực tê
ta có pt
3200/x-3=(5+(3200-5x)/(x+40))

Gọi nâng suất ban đầu là x
=>THời gian dự định là 100/x
Theo đề, ta có: 100/x=40/x-2+60/2x
=>70/x=40/x-2
=>70x-140=40x
=>30x=140
=>x=14/3
=>Thời gian dự định là 100:14/3=100*3/14=300/14=150/7(ngày)

Gọi số công nhân lúc đầu là x (người) và số sản phẩm mỗi công nhân dự tính làm được lúc đầu là y (sản phẩm) (x, y > 0)
Theo dự tính lúc đầu: xy = 360 (*)
Khi điều 3 công nhân đi và mỗi công nhân còn lại phải làm nhiều hơn dự định 4 sản phẩm, ta có phương trình: (x-3)(y + 4) = 360
⇒ xy + 4x - 3y - 12 = 360. Thay (*) vào ta được:
⇒ xy + 4x - 3y - 12 = xy
⇒4x - 3y = 12 => x = 12+3y412+3y4. Thay x vào (*) ta được:
\(\dfrac{12x+3y}{4}y\) = 360
12y + 3y2 = 1440
y2 + 4y - 480 = 0
(y+2)2 = 484
y + 2 = 22 hoặc y + 2 = -22 (loại vì y > 0)
y = 20
⇒ x = 18
Tham khảo

Lời giải:
Giả sử theo kế hoạch mỗi ngày người đó dự định may $a$ khẩu trang.
ĐK: $a\in\mathbb{N}^*$
Thời gian dự định: $\frac{1000}{a}$ (ngày)
Thực tế:
Mỗi ngày người đó may: $a+30$ (khẩu trang)
Số ngày may: $\frac{1000}{a}-1$ (ngày)
Số khẩu trang thực tế:
$(a+30)(\frac{1000}{a}-1)=1000+170$
$\Leftrightarrow a^2+200a-30000=0$
$\Rightarrow a=100$
Vậy mỗi ngày người đó dự định may 100 khẩu trang.

Gọi năng suất dự định là x (0 < x < 20, sản phẩm/giờ)
Sản phẩm làm được sau 2 giờ là: 2x (sản phẩm)
Số sản phẩm còn lại là 120 – 2x (sản phẩm)
Năng suất sau khi cải tiến là x + 3 (sản phẩm/giờ)
Thời gian làm số sản phẩm còn lại là: 120 - 2 x x + 3 (giờ)
Do sau khi cải tiến người đó hoàn thành kế hoạch sớm hơn dự định 1 giờ 36 phút
Đổi 1 giờ 36 phút bằng 1,6 giờ
Theo bài ra ta có phương trình:
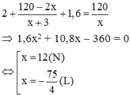
Vậy năng suất dự định của công nhân đó là 12 sản phẩm/giờ
Đáp án C

Lời giải:
Giả sử năng suất ban đầu là $a$ sản phẩm/ ngày.
Số ngày dự định: $\frac{300}{a}$ (ngày)
Năng suất sau khi tăng: $a+5$ (sản phẩm/ ngày)
Số ngày hoàn thành sản phẩm: $\frac{300}{a+5}$ (ngày)
Theo bài ra: $\frac{300}{a}-\frac{300}{a+5}=3$
Giải pt trên, với điều kiện $a>0$ suy ra $a=20$
Vậy theo kế hoạch thì người thợ đó làm 20sp/ ngày
Gọi số sản phẩm phải làm trong 1 ngày là x
Theo đề, ta có: \(\dfrac{300}{x}-\dfrac{300}{x+5}=3\)
=>100/x-100/x+5=1
=>(100x+500-100x)/(x^2+5x)=1
=>x^2+5x-500=0
=>(x+25)(x-20)=0
=>x=20