Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
Có 2 bộ số {a;b;c} có tổng các chữ số bằng 5 là: {0;1;4}, {0;2;3}, mỗi bộ số có 3! hoán vị nên có tất cả 12 khả năng.
Do đó xác suất để người đó bấm máy một lần đúng số cần gọi là 1 12 .
Tham khảo:
Số phần tử của không gian mẫu là 
. Để người đó gọi đúng số điện thoại mà không phải thử quá hai lần ta có 2 trường hợp:
TH1: Người đó gọi đúng ở lần thứ nhất.
TH2: Người đó gọi đúng ở lần thứ hai. Gọi A1 người đó gọi đúng ở lần thứ nhất
Xác suất người đó gọi đúng là P(A1) = \(\dfrac{1}{10}\)
Xác suất người đó gọi không đúng là P(A1) = \(\dfrac{9}{10}\).
Gọi A2 là người đó gọi đúng ở lần thứ hai
Xác suất người đó gọi đúng là P(A2) = \(\dfrac{1}{9}\) .
Gọi A là người đó gọi đúng số điện thoại mà không phải thử quá hai lần, ta có 
(đpcm)
Chọn D
Gọi 2 số cuối là ab,là số điện thoại nên có đủ các chữ số từ 0 đến 9
Ta có a có 10 cách chọn, b khác a nên có 9 cách chọn. Vậy không gian mẫu có 9.10= 90 phần tử.
Vậy xá xuất gọi một lần dúng là 1/90
Chọn A
+ Số các chỉnh hợp chập của tập hợp các chữ số 
Số các chỉnh hợp chập của tập hợp các chữ số {0;1;2;3;4;5;6;7;8;9} mà chữ số 0 đứng vị trí đầu tiên ( 0 b c ¯ ) bằng số các chỉnh hợp chập của tập hợp các chữ số {0;1;2;3;4;5;6;7;8;9} và bằng A 9 2 .
Suy ra số các số tự nhiên có chữ số đôi một khác nhau bằng 
+ Lấy ngẫu nhiên ra từ hai số có 
cách.
+ Gọi là biến cố “lấy được từ hai số mà các chữ số có mặt ở hai số đó giống nhau”
Trường hợp 1: Ba chữ số có mặt trong hai số được lấy không có chữ số 0
Chọn ba chữ số trong tập {0;1;2;3;4;5;6;7;8;9} có C 9 3 cách.
Ba chữ số này tạo thành 3! = 6 số trong A.
Lấy hai số trong 6 số này có C 6 2 cách (hai số các chữ số có mặt ở hai số đó giống nhau).
Suy ra có C 9 3 . C 6 2 cách lấy hai số thỏa trường hợp 1.
Trường hợp 2: Ba chữ số có mặt trong hai số được lấy có chữ số .
Chọn thêm hai chữ số trong tập {0;1;2;3;4;5;6;7;8;9}có C 9 2 cách.
Ba chữ số này (hai chữ số vừa chọn và chữ số 0) tạo thành 2.2! = 4 số trong A.
Lấy hai số trong 4 số này có C 4 2 (hai số các chữ số có mặt ở hai số đó giống nhau).
Suy ra có C 9 2 . C 4 2 cách lấy hai số thỏa trường hợp 2.
Suy ra 
+ Do đó, xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau là:
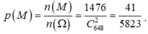
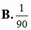
n(A)=1
\(n\left(\Omega\right)=C^1_{10}\cdot C^1_9=90\)
=>Xác suất đúng là 1/90