Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Rõ ràng trong hộp có 30 quả với 15 quả ghi số chẵn, 10 quả màu đỏ, 5 quả màu đỏ ghi số chẵn, 25 quả màu xanh hoặc ghi số lẻ. Vậy theo định nghĩa
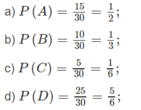
Trong đó A, B, C, D là các biến cố tương ứng với các câu a), b), c) ,d).

Chọn D
Chọn ngẫu nhiên một quả trong 30 quả có 30 cách. Vậy n ( Ω ) = 30.
Gọi A là biến cố: “lấy được quả cầu màu xanh”.
Ta có n(A) = 20 => P(A) = 2 3
Gọi B là biến cố: “lấy được quả cầu ghi số lẻ”.
Ta có n(B) = 15 => P(B) = 1 2 .
Số quả cầu vừa màu xanh vừa ghi số lẻ: 10 (quả).
Xác suất để lấy được quả cầu vừa màu xanh vừa ghi số lẻ: 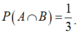
Xác suất để lấy được quả cầu màu xanh hay ghi số lẻ:
![]()
![]()

Kí hiệu A là biến cố : "Quả lấy ra mầu đỏ"
B là biến cố : "Quả lấy ra ghi số chẵn"
a) Không gian mẫu \(\Omega=\left\{1,2,...,10\right\}\)
\(A=\left\{1,2,3,4,5,6\right\}\)
Từ đó : \(P\left(A\right)=\dfrac{6}{10}=\dfrac{3}{5}\)
Tiếp theo, \(B=\left\{2;4;6;8;10\right\}\) và \(A\cap B=\left\{2;4;6\right\}\)
Do đó : \(P\left(B\right)=\dfrac{5}{10}=\dfrac{1}{2};P\left(AB\right)=\dfrac{3}{10}\)
Ta thấy \(P\left(AB\right)=\dfrac{3}{10}=\dfrac{3}{5}.\dfrac{1}{2}=P\left(A\right)P\left(B\right)\)
Vậy A và B độc lập.

Kí hiệu A là biến cố: "Quả lấy ra màu đỏ";
B là biến cố: "Quả lấy ra ghi số chẵn".
Không gian mẫu
Ω = {1, 2, ..., 10};
A = {1, 2, 3, 4, 5, 6}.
Từ đó: 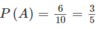
Tiếp theo: B = {2, 4, 6, 8, 10} và A ∩ B = {2, 4, 6}.
Do đó: 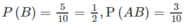
Ta thấy
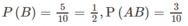
Vậy A và B độc lập.

Số quả xanh mang số lẻ: 8 quả
\(\Rightarrow\) số quả cầu có màu đỏ hoặc mang số lẻ: \(20+8=28\)
Xác suất: \(P=\frac{28}{35}=\frac{4}{5}\)

Không gian mẫu: \(C_{15}^3=455\)
Số cách chọn 3 quả sao cho vừa khác màu vừa khác số:
\(4.4.4=64\)
Xác suất: \(P=\dfrac{64}{455}\)
Trong hộp có 30 quả với 15 quả ghi số chẵn, 10 quả mầu đỏ, 5 quả mầu đỏ ghi số chẵn, 25 quả mầu xanh hoặc ghi số lẻ. Vậy theo định nghĩa :
a) \(P\left(A\right)=\dfrac{15}{30}=\dfrac{1}{2}\)
b) \(P\left(B\right)=\dfrac{10}{30}=\dfrac{1}{3}\)
c) \(P\left(C\right)=\dfrac{5}{30}=\dfrac{1}{6}\)
d) \(P\left(D\right)=\dfrac{25}{30}=\dfrac{5}{6}\)