Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Từ giả thiết ta có: r = a; 2a.h = 2 a 2 => h = a => Sxq = 2πrh = 2π a 2

a, Diện tích của mặt cầu là: \(S_c=4\pi r^2\)
Diện tích xung quanh của mặt trụ là: \(S_t=2\pi rh=4\pi r^2\)
Vậy Sc = St
b, Thể tích của khối trụ là: \(V_t=\pi r^2h=2\pi r^2\)
Thể tích của khối cầu là: \(V_c=\dfrac{4}{3}\pi r^2\)
Vậy \(V_t=\dfrac{3}{2}V_c\)

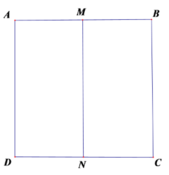
Mặt trụ tạo bởi hình vuông ABCD khi quay quanh MN có đường cao h = a và bán kính đáy ![]()
Diện tích 1 đáy và diện tích xung quanh của hình trụ là:
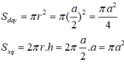
Nên có diện tích toàn phần của hình trụ:
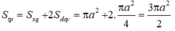
Mặt cầu (S) có bán kính R có diện tích bằng Stp của mặt trụ nên:
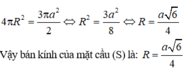



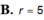
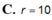


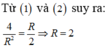
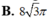

Chọn A.
Gọi r là bán kính đáy của hình trụ, h là chiều cao của hình trụ.
Theo bài ra ta có:
S = 2 π r h π r 2 = 4 π a 2 ⇔ r = 2 a h = S 4 π a
Thể tích khối trụ là:
V = π r 2 h = π 4 a 2 · S 4 π a = S a