Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1,gọi chiều rộng mảnh vườn là x(m)
chiều dài mảnh vườn là x+3 (m) (x>0)
vì tăng chiều dài thêm 2m và giảm chiều rộng 1m thì diện tích mảnh vườn không đổi nên ta có pt:
(x-1)(x+5)=x(x+3)
⇔\(x^2+5x-x-5=x^2+3x\Leftrightarrow x^2-x^2+5x-x-3x=5\Leftrightarrow x=5\) (TM)
vậy chiều rộng mảnh vườn là 5m
chiều dài mảnh vườn là 5+3=8m
2,bán kính đáy của hình trụ là 1,2:2= 0,6 (m)
thể tích của hình trụ là : V = 3,14.(0,6)\(^2\).1,8=2 (m\(^3\))
vậy thể tích của hình trụ đó là 2m\(^3\)

Diện tích đám đất là:
1/2(30+50)*40=20*80=1600m2
Diện tích trồng rau là:
1600*2/5=640m2

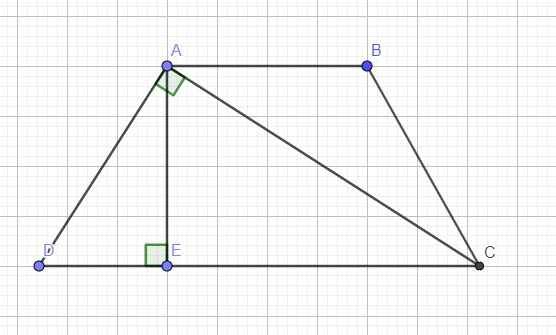
Kẻ đường cao góc AE \(\Rightarrow AE=AB\)
Lại có ABCD là hình thang cân \(\Rightarrow CD=AB+2DE=AE+2DE\Rightarrow DE=\dfrac{CD-AE}{2}=\dfrac{10-AE}{2}\)
\(EC=AB+DE=AE+DE=AE+\dfrac{10-AE}{2}=\dfrac{AE+10}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACD có:
\(AE^2=DE.EC\Leftrightarrow AE^2=\left(\dfrac{10-AE}{2}\right)\left(\dfrac{10+AE}{2}\right)\)
\(\Leftrightarrow4AE^2=100-AE^2\Rightarrow AE=2\sqrt{5}\) \(\Rightarrow AB=2\sqrt{5}\)
\(S_{ABCD}=\dfrac{1}{2}AE.\left(AB+CD\right)=\dfrac{1}{2}.2\sqrt{5}.\left(2\sqrt{5}+10\right)=...\)

Câu 11.12.
Kẻ đường cao \(AH,BK\).
Do tam giác \(\Delta AHD=\Delta BKC\left(ch-gn\right)\)nên \(DH=BK\).
Đặt \(AB=AH=x\left(cm\right),x>0\).
Suy ra \(DH=\frac{10-x}{2}\left(cm\right)\)
Xét tam giác \(AHD\)vuông tại \(H\):
\(AD^2=AH^2+HD^2=x^2+\left(\frac{10-x}{2}\right)^2\)(định lí Pythagore)
Xét tam giác \(DAC\)vuông tại \(A\)đường cao \(AH\):
\(AD^2=DH.DC=10.\left(\frac{10-x}{2}\right)\)
Suy ra \(x^2+\left(\frac{10-x}{2}\right)^2=10.\frac{10-x}{2}\)
\(\Leftrightarrow x=2\sqrt{5}\)(vì \(x>0\))
Vậy đường cao của hình thang là \(2\sqrt{5}cm\).
Câu 11.11.
Kẻ \(AE\perp AC,E\in CD\).
Khi đó \(AE//BD,AB//DE\)nên \(ABDE\)là hình bình hành.
Suy ra \(AE=BD=15\left(cm\right)\).
Kẻ đường cao \(AH\perp CD\)suy ra \(AH=12\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AH\):
\(\frac{1}{AH^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AE^2}=\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AC=20\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.15.20=150\left(cm^2\right)\),

Ta có hình vẽ và các điểm tương ứng. Gọi x là chiều rông 2 con đường, đk : 0<x<15
Hình thang GHIK là hình thang cân, có đáy lớn cộng đáy nhỏ bằng 2MN = AB + DC = 80
Vậy \(S_{GHIK}=\frac{80.2x}{2}=80x\)
PQRS là hình bình hành nên diện tích bằng: \(2x.35=70x\)
Phần gạch chéo là hình bình cạnh đáy 2x, chiều cao 2x nên diện tích là \(2x.2x=4x^2\)
Vậy diện tích hình GPQHIRSK bằng: \(S_{GHIK}+S_{PQRS}\)- S phần gạch chéo = \(80x+70x-4x^2=\frac{1}{4}\frac{80.35}{2}\Rightarrow-4x^2+150x-350=0\Rightarrow\orbr{\begin{cases}x=2,5\\x=35\left(L\right)\end{cases}}\)

Chiều cao mảnh đất hình thang là :
48 x 2 : (3 + 5) = 12 (m)
Tổng độ dài hai đáy là :
357,6 x 2 : 12 = 59,6 (m)
Độ dài đáy bé là :
(59,6 - 8,8) : 2 = 25,4 (m)
Độ dài đáy lớn là :
59,6 - 25,4 = 34,2 (m)
Đáp số : Đáy bé : 25,4 m
Đáy lớn : 34,2 m
88 m
ai tk mk
mk nhất định sẽ tk lại người đó
hứa luôn
thank nhiều
Đáy phải là :
90 x 2 : 10 = 18 ( m )
Khi mở rộng đáy tam giác trái là :
22 - 18 = 4 ( m )
Diện tích mở rộng phần đất bên trái là :
4 x 10 : 2 = 20 ( m2 )
Diện tích phần được mở rộng là :
20 + 90 = 110 ( m2 )
Diện tích thửa ruộng là :
110 x 7 = 770 ( m2 )
Tổng 2 đáy là :
770 x 2 : 10 = 154 ( m )
Đáy lớn hình thang là :
( 154 + 22 ) : 2 = 88 ( m )
Đáp số : 88 m