Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

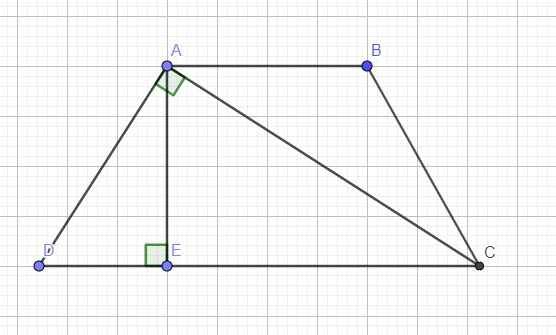
Kẻ đường cao góc AE \(\Rightarrow AE=AB\)
Lại có ABCD là hình thang cân \(\Rightarrow CD=AB+2DE=AE+2DE\Rightarrow DE=\dfrac{CD-AE}{2}=\dfrac{10-AE}{2}\)
\(EC=AB+DE=AE+DE=AE+\dfrac{10-AE}{2}=\dfrac{AE+10}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACD có:
\(AE^2=DE.EC\Leftrightarrow AE^2=\left(\dfrac{10-AE}{2}\right)\left(\dfrac{10+AE}{2}\right)\)
\(\Leftrightarrow4AE^2=100-AE^2\Rightarrow AE=2\sqrt{5}\) \(\Rightarrow AB=2\sqrt{5}\)
\(S_{ABCD}=\dfrac{1}{2}AE.\left(AB+CD\right)=\dfrac{1}{2}.2\sqrt{5}.\left(2\sqrt{5}+10\right)=...\)

Kẻ AH vuông góc với BC, BK vuông góc với CD, đường chéo AC vuông góc với AD.
Đặt AH = AB = x => AH = x
Tam giác AHD = tam giác BKC ( c.h - g.n)
=> DH = CK = (10-x)/2
Vậy HC = Hk + CK = x + (10-x)/2 = (x-10)/2
Áp dụng hệ thức lượng trong tam giác ADC vuông tại A
Có AH^2 = DH.HC => x^2 = (10-x)/2 . (x-10)/2
=> 5x^2 = 20
=> x = 2√ 5
Vậy AH = 2√5

a) tính đường cao AH:
xét tam giác DHA vuông tại H có sin góc DAH = DH/AD
=>DH=AD. sin65
Từ đó suy ra AH theo pitago
hạ đường cao CE từ C xuống cạnh AB
KHi đó CD=EH=AB - 2AH
b)góc ABD chính là góc HBD trong tam giác HBD vuông tại H
=>tan HBD= DH/HB=DH/(AB-AH)
=>góc HBD
Tính đường chéo BD theo pitago trong tgiac DHBvuông tại H
a) tính đường cao AH:
xét tam giác DHA vuông tại H có sin góc DAH = DH/AD
=>DH=AD. sin65
Từ đó suy ra AH theo pitago
hạ đường cao CE từ C xuống cạnh AB
KHi đó CD=EH=AB - 2AH
b)góc ABD chính là góc HBD trong tam giác HBD vuông tại H
=>tan HBD= DH/HB=DH/(AB-AH)
=>góc HBD
Tính đường chéo BD theo pitago trong tgiac DHBvuông tại H