Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì của con lắc khi không có điện trường và khi có điện trường hướng thẳng đứng:
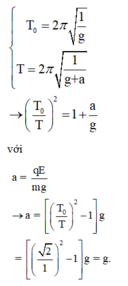
Chu kì của con lắc khi điện trường có hướng hợp với g một góc 60 o
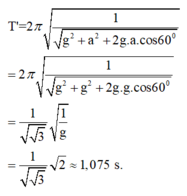
Đáp án A

Tích điện âm cho con lắc, rồi thả vào điện trường hướng thẳng xuống
→ Lực điện ngược hướng trọng lực
→ \(g'=\frac{mg-qE}{m}\)
\(\frac{T_2}{T_1}=\sqrt{\frac{g}{g'}}=2\) → \(\frac{mg}{mg-qE}=4\Rightarrow qE=\frac{3}{4}mg\)
Đảo chiều điện trường
→ Lực điện cùng hướng trọng lực
→ \(g''=\frac{qE+mg}{m}=\frac{\frac{7}{4}mg}{m}=\frac{7}{4}g\)
\(\frac{T_1}{T}=\sqrt{\frac{g''}{g}}=\sqrt{\frac{qE+mg}{mg}}=\sqrt{\frac{7}{4}}\Rightarrow T\approx2,51\)
Không biết có sai sót gì k :p

Đáp án A
+ Chu kì dao động của con lắc khi không có và có điện trường:
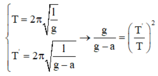
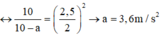

Chu kì: \(T=2\pi\sqrt{\frac{l}{g}}\Rightarrow\frac{1}{T^2}=k.g\)(k là hệ số tỉ lệ)
Khi không có điện trường: \(\frac{1}{T_0^2}=k.g\) (1)
Giả sử khi điện trường hướng xuống dưới: \(g_1=g+a\) (do lực điện là lực lạ nên cùng phương với trọng lực nên ta có mối liên hệ như vậy, a có thể âm hoặc đương)
Do vậy, khi điện trường hướng lên trên: \(g_2=g-a\)
Ta có:
\(\frac{1}{T_1^2}=k\left(g+a\right)\) (2)
\(\frac{1}{T_2^2}=k\left(g-a\right)\)(3)
Lấy (2) cộng (3) vế với vế, ta đc: \(\frac{1}{T_1^2}+\frac{1}{T_2^2}=2.k.g=\frac{2}{T_0^2}\)
Đáp án B.

Đáp án A
Cần lưu ý: Chu kì của con lắc lo xo (CLLX)
chỉ phụ thuộc vào độ cứng k và khối lượng m.
Do đó khi đặt vào trong điện trường đều thì chu kì CLLX không thay đổi. Chu kì của con lắc đơn phụ thuộc vào gia tốc trọng trường nơi treo con lắc.
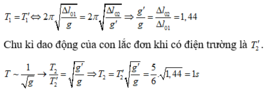

Đáp án B
Khi con lắc dao động trong điện trường, nó dao động dưới tác dụng của trọng lực biểu kiến:
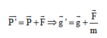

=> Lực điện trường phải hướng lên
Mà F → = q E → n ê n F → hướng lên khi
+ q > 0 và điện trường hướng lên
+ q < 0 và điện trường hướng xuống.
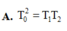
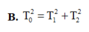
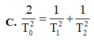
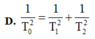
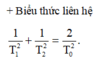


Đáp án C