Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải thích: Đáp án D
Phương pháp: Sử dụng lí thuyết về dao động điều hòa của con lắc đơn kết hợp với chuyển động ném ngang
Cách giải:
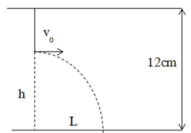
Gọi khoảng cách từ VTCB của con lắc đến mặt nước là h => dây treo con lắc có chiều dài l = 12 – h
Vận tốc của con lắc khi đi qua VTCB: 
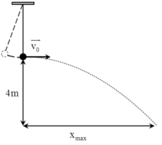
Tại đây, dây treo con lắc bị đứt => con lắc sẽ chuyển động như một vật bị ném ngang với vận tốc ban đầu v0
=> Tầm bay xa: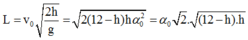 
Nhận xét: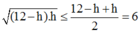 
(theo cô-si) 
Vậy Lmax = 85cm => Chọn D
Giải thích: Đáp án D
Phương pháp: Áp dụng công thức tính vận tốc của con lắc đơn
Cách giải:
Chu kỳ dao động của con lắc: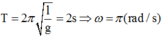 
Thời điểm sợi dây treo con lắc bị đứt là t0 = T/4 = 0,5s
Vậy thời điểm t = 0,08s con lắc chưa bị đứt.
PT dao động của con lắc: 
Khi t = 0,08s thì α = 0,087 rad
Tốc độ của vật nặng khi đó: 
Đáp án B
Tốc độ của con lắc khi đi qua VTCB
Tầm ném bay xa của vật theo phương ngang
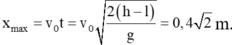
Vậy khoảng cách từ vị trí tuột dây đến vị trí chạm đất
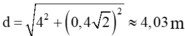
Đáp án B
+ Chu kì của con lắc vướng đinh T = π l 0 g + π 0 , 5 l 0 g = 2 , 4
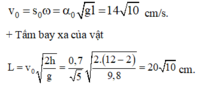
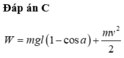
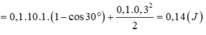
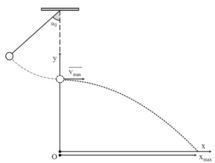
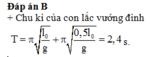
Ta có hình vẽ:
Chọn mốc tính thế năng ở vị trí cân bằng.
Ta có thể tính được độ cao h của vật ở vị trí ban đầu so với vị trí cân bằng.
Áp dụng định luật bảo toàn cơ năng, cho vị trí ban đầu và vị trí cân bằng của quả nặng, ta có:
Đến vị trí cân bằng, con lắc bị đứt dây nên nó sẽ chuyển động như 1 vật bị ném ngang với vận tốc ban đầu là v.
Khoảng cách từ vị trí vật chạm đất đến vị trí thẳng đứng từ vị trí cân bằng là tầm bay xa của vật
Áp dụng công thức:
Đáp án B