
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
b: \(10^6-5^7=5^6\left(2^6-5\right)=5^6\cdot59⋮59\)

a. \(a\left(a-1\right)-\left(a+3\right)\left(a+2\right)=a^2-a-\left(a^2+5a+6\right)=-6a-6=6\left(-a-1\right)⋮6\)
b. \(a\left(a+2\right)-\left(a-5\right)\left(a-7\right)=a^2+2a-\left(a^2-12a+35\right)=14a-35=7\left(2a-5\right)⋮7\)
c. \(\left(n^2-3n+1\right)\left(n+2\right)-n^3+n^2+3=n^3-n^2-5n+2-n^3+n^2+3=-5n+5\)
\(=5\left(1-n\right)⋮5\)
a) \(a\left(a-1\right)-\left(a+3\right)\left(a+2\right)=a^2-a-a^2-5a-6=-6a-6=-6\left(a+1\right)⋮6,\forall a\in Z\)
b) \(a\left(a+2\right)-\left(a-5\right)\left(a-7\right)=a^2+2a-a^2+12a-35=14a-35=7\left(2a-5\right)⋮7,\forall a\in Z\)c) \(\left(n^2-3n+1\right)\left(n+2\right)-n^3+n^2+3=n^3-n^2-5n+2-n^3+n^2+3=-5n+5=-5\left(n-5\right)⋮5,\forall n\in Z\)

Đề bài thiếu bạn nhé, có lẽ là x và y là các số nguyên.



word:
-vùng soạn thảo
- con trỏ văn bản
- thước ngang
- thước dọc
Excel:
-trang tính
- thanh công cụ
- bảng chọn Data
- tên cột, tên hàng
- ô tính
Cho mik 1 tích nha !!

Ta thấy rằng 2|y+1| luôn luôn lớn hơn 0
Nên suy ra được là : |x-3|+2(y+1)=6
<=>|x-3|+2y=4
<=>|x-3|=4-2y
Có hai trường hợp
1, x-3=4-2y
<=>x-7-2y=0
<=>x-2y=7
2, 3-x=4-2y
<=>x-2y=-1
Đến đây ta thấy hai kết quả khác hoàn toàn nên ko thảo mãn x và y
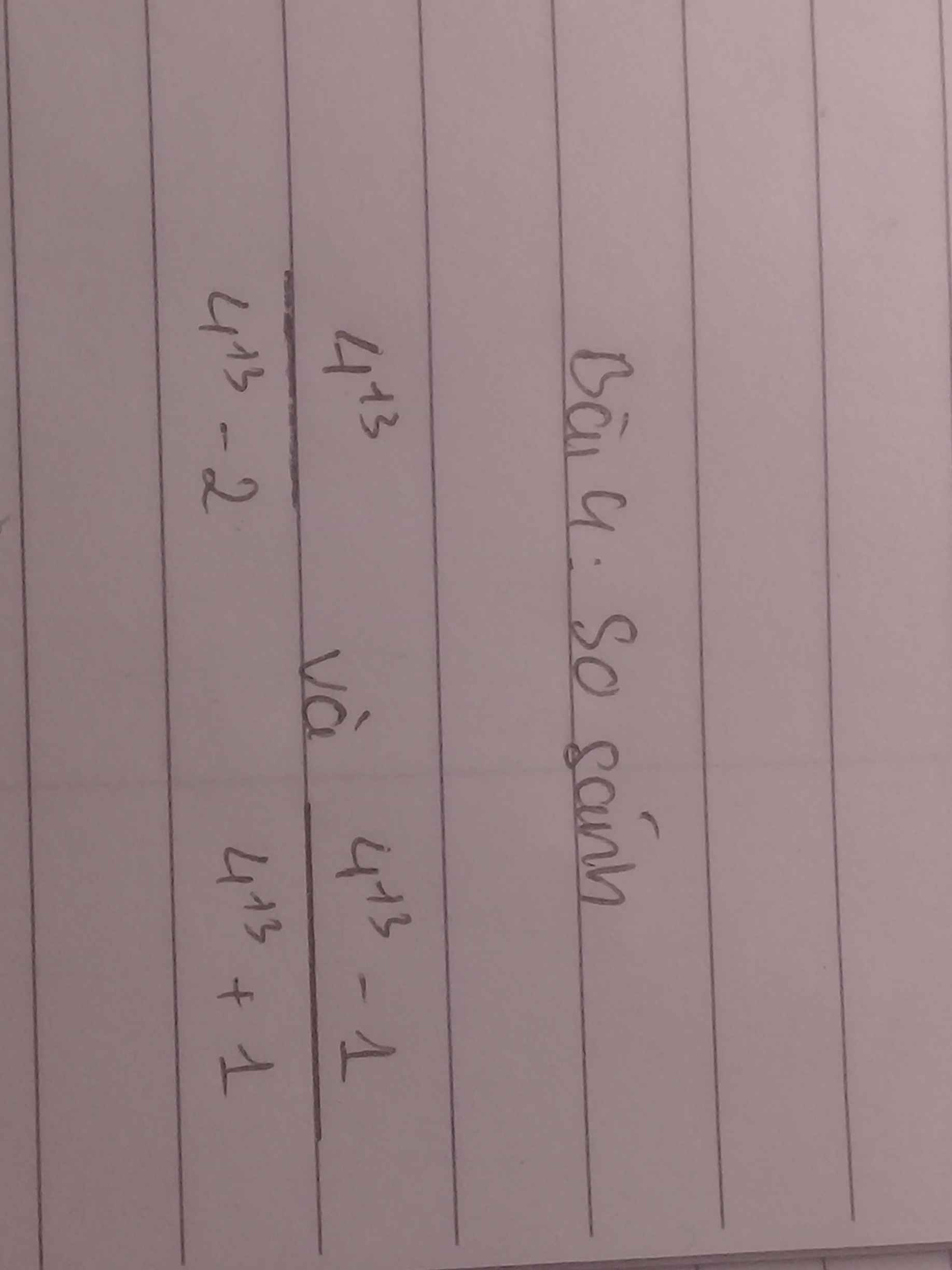

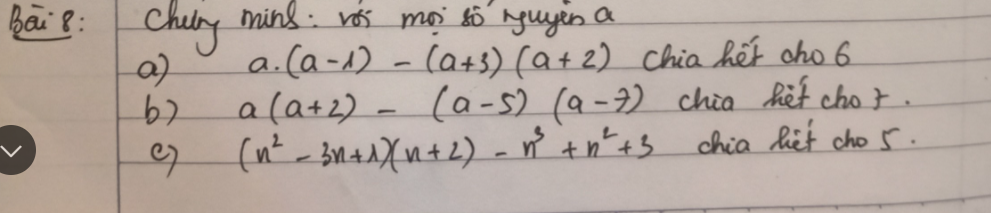
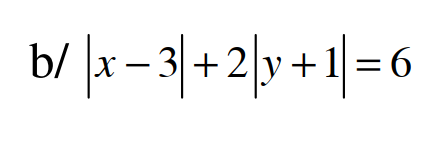


\(\dfrac{4^{13}}{4^{13}-2}=1+\dfrac{2}{4^{13}-2}\)
\(\dfrac{4^{13}-1}{4^{13}+1}=1-\dfrac{2}{4^{13}+1}\)
Do \(4^{13}-2< 4^{13}+1\Rightarrow\dfrac{2}{4^{13}-2}>\dfrac{2}{4^{13}+1}\Rightarrow\dfrac{2}{4^{13}-2}>-\dfrac{2}{4^{13}-1}\)
\(\Rightarrow\dfrac{4^{13}}{4^{13}-2}>\dfrac{4^{13}-1}{4^{13}+1}\)
Ta có:
\(\dfrac{4^{13}}{4^{13}-2}=\dfrac{4^{13}-2}{4^{13}-2}+\dfrac{2}{4^{13}-2}=1+\dfrac{2}{4^{13}-2}\)
\(\dfrac{4^{13}-1}{4^{13}+1}=\dfrac{4^{13}+1}{4^{13}+1}-\dfrac{2}{4^{13}+1}=1-\dfrac{2}{4^{13}+1}\)
Vì \(1+\dfrac{2}{4^{13}-2}>1-\dfrac{2}{4^{13}+1}\)
⇒\(\dfrac{4^{13}}{4^{13}-2}>\)\(\dfrac{4^{13}-1}{4^{13}+1}\)