K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 8 2021
a) Gọi 3 số chẵn liên tiếp lần lượt là: \(2x,2x+2,2x+4\)
Theo đề bài ta có phương trình:
\(\left(2x+2\right)\left(2x+4\right)-2x\left(2x+2\right)=192\Rightarrow4x^2+12x+8-4x^2-4x=192\Rightarrow8x=184\Rightarrow x=23\)
Vậy 3 số chẵn liên tiếp đó lần lượt là: 46, 48, 50
b) Gọi 4 số tự nhiên liên tiếp đó lần lượt là: x, x+1, x+2, x+3
Theo đề bài ta có phương trình:
\(\left(x+2\right)\left(x+3\right)-x\left(x+1\right)=146\Rightarrow x^2+5x+6-x^2-x=146\Rightarrow4x=140\Rightarrow x=35\)
Vậy 4 số tự nhiên liên tiếp đó lần lượt là: 35,36,37,38
19 tháng 6 2023
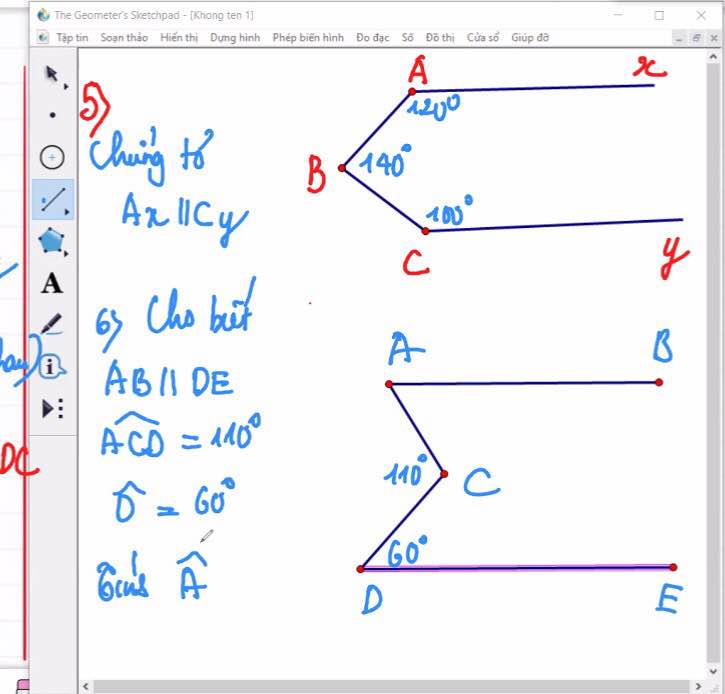
3:
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
=>DB=ED
b; Xét ΔDBK và ΔDEC có
góc DBK=góc DEC
DB=DE
góc BDK=góc EDC
=>ΔDBK=ΔDEC
c: AB+BK=AK
AE+EC=AC
mà AB=AE; BK=EC
nên AK=AC
=>ΔAKC cân tại A
d: ΔAKC cân tại A
mà AD là phân giác
nên AD vuông góc KC
NT
6 tháng 9 2021
c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
KK
6 tháng 9 2021
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)
TC
0
XO
7 tháng 5 2021
Để B có nghiệm
=> B = 0
=> 2x4 - 8x2 = 0
=> 2x2(x2 - 4) = 0
=> \(\orbr{\begin{cases}2x^2=0\\x^2-4=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=\pm2\end{cases}}\)
Vậy x \(\in\left\{0;2;-2\right\}\)là nghiệm của đa thức B
16 tháng 12 2021
Bài 3:
b: \(10^6-5^7=5^6\left(2^6-5\right)=5^6\cdot59⋮59\)
25 tháng 9 2021
\(\dfrac{4^{13}}{4^{13}-2}=1+\dfrac{2}{4^{13}-2}\)
\(\dfrac{4^{13}-1}{4^{13}+1}=1-\dfrac{2}{4^{13}+1}\)
Do \(4^{13}-2< 4^{13}+1\Rightarrow\dfrac{2}{4^{13}-2}>\dfrac{2}{4^{13}+1}\Rightarrow\dfrac{2}{4^{13}-2}>-\dfrac{2}{4^{13}-1}\)
\(\Rightarrow\dfrac{4^{13}}{4^{13}-2}>\dfrac{4^{13}-1}{4^{13}+1}\)
MH
25 tháng 9 2021
Ta có:
\(\dfrac{4^{13}}{4^{13}-2}=\dfrac{4^{13}-2}{4^{13}-2}+\dfrac{2}{4^{13}-2}=1+\dfrac{2}{4^{13}-2}\)
\(\dfrac{4^{13}-1}{4^{13}+1}=\dfrac{4^{13}+1}{4^{13}+1}-\dfrac{2}{4^{13}+1}=1-\dfrac{2}{4^{13}+1}\)
Vì \(1+\dfrac{2}{4^{13}-2}>1-\dfrac{2}{4^{13}+1}\)
⇒\(\dfrac{4^{13}}{4^{13}-2}>\)\(\dfrac{4^{13}-1}{4^{13}+1}\)
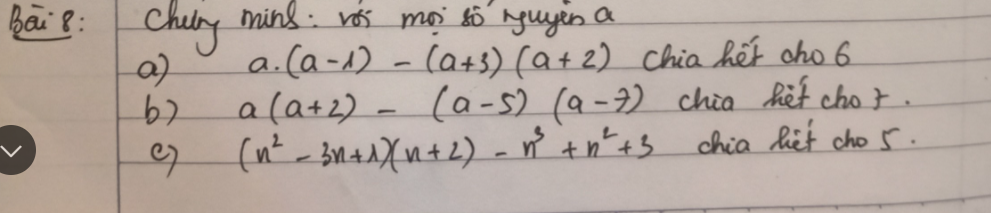
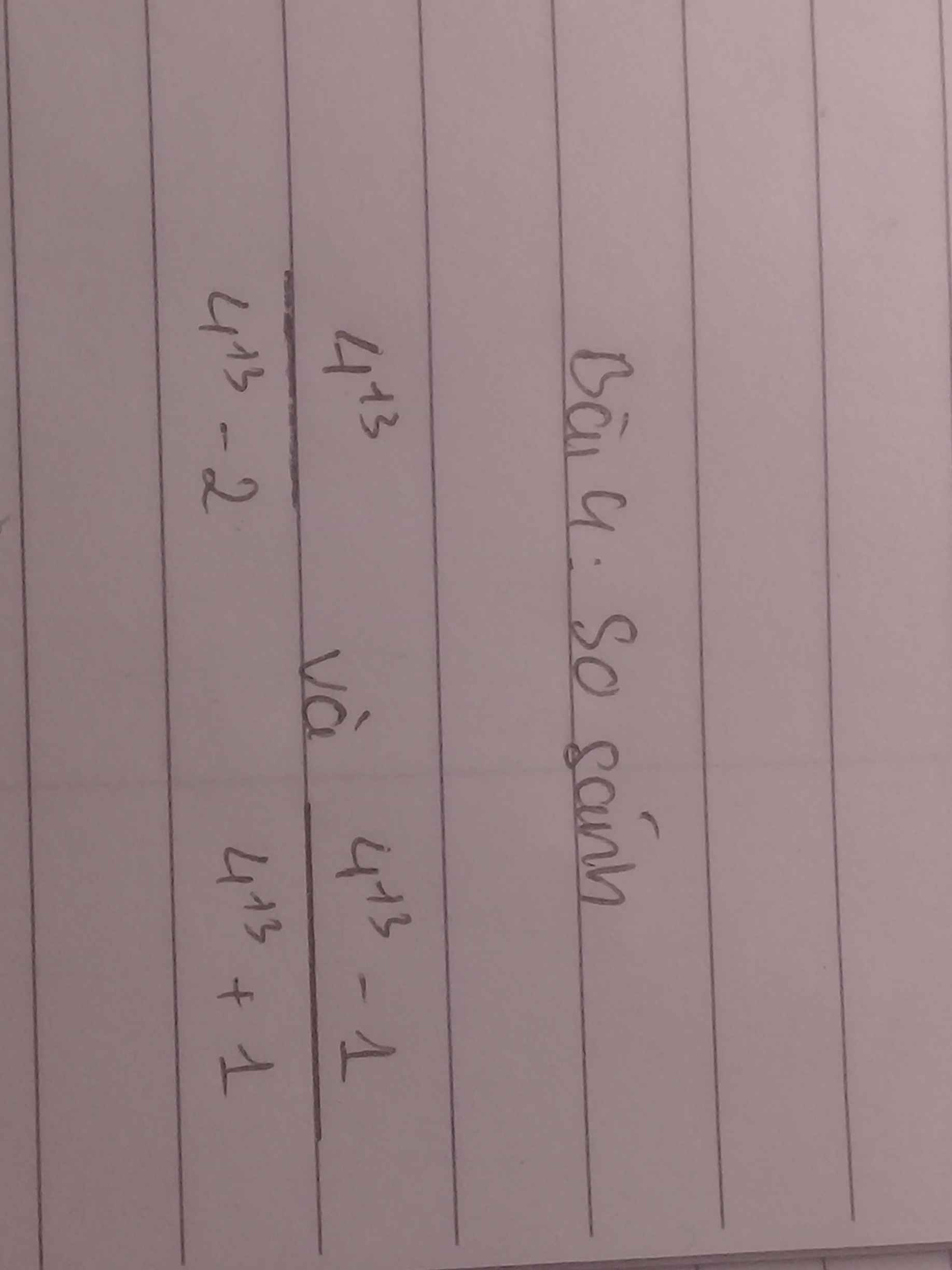
a. \(a\left(a-1\right)-\left(a+3\right)\left(a+2\right)=a^2-a-\left(a^2+5a+6\right)=-6a-6=6\left(-a-1\right)⋮6\)
b. \(a\left(a+2\right)-\left(a-5\right)\left(a-7\right)=a^2+2a-\left(a^2-12a+35\right)=14a-35=7\left(2a-5\right)⋮7\)
c. \(\left(n^2-3n+1\right)\left(n+2\right)-n^3+n^2+3=n^3-n^2-5n+2-n^3+n^2+3=-5n+5\)
\(=5\left(1-n\right)⋮5\)
a) \(a\left(a-1\right)-\left(a+3\right)\left(a+2\right)=a^2-a-a^2-5a-6=-6a-6=-6\left(a+1\right)⋮6,\forall a\in Z\)
b) \(a\left(a+2\right)-\left(a-5\right)\left(a-7\right)=a^2+2a-a^2+12a-35=14a-35=7\left(2a-5\right)⋮7,\forall a\in Z\)c) \(\left(n^2-3n+1\right)\left(n+2\right)-n^3+n^2+3=n^3-n^2-5n+2-n^3+n^2+3=-5n+5=-5\left(n-5\right)⋮5,\forall n\in Z\)