K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 12 2018
Gọi số hoa của 3 bạn lần lượt là x, y , z
Vì x,y,z TLT vớ 4,5,6
=> x/4=y/5=z/6=k
Theo t/c dãy tỉ số bằng nhau :
k= x+y+z/ 4+5+6 = 75/15=5
=> x= 5.4=20
y= 5. 5 = 25
z= 5.6=30
Vậy ..
BN
12 tháng 12 2018
Gọi số hoa 3 bạn hái được lần lượt là a,b,c \(\left(a,b,c\inℕ^∗\right)\)
Theo đề bài ra,ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ,ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{a+b+c}{4+5+6}=\frac{75}{15}=6\)
\(\Rightarrow\hept{\begin{cases}a=6.4=24\\b=6.5=30\\c=6.6=36\end{cases}}\)
Vậy ....
8 tháng 10 2021
\(\widehat{B_2}=\widehat{B_4}=60^0\left(đối.đỉnh\right)\\ \widehat{B_2}+\widehat{B_1}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{B_1}=180^0-60^0=120^0\\ \Rightarrow\widehat{B_3}=\widehat{B_1}=120^0\left(đối.đỉnh\right)\)
Vì a//b nên \(\widehat{B_2}=\widehat{A_4}=60^0;\widehat{B_1}=\widehat{A_3}=120^0\left(so.le.trong\right)\)
Ta có \(\left\{{}\begin{matrix}\widehat{A_2}=\widehat{A_4}=60^0\\\widehat{A_1}=\widehat{A_3}=120^0\end{matrix}\right.\left(đối.đỉnh\right)\)
W
1
25 tháng 12 2018
=1(1+1) + 2(2+1) + 3(3+1) +...+n(n+1)
=(1^2 + 2^2 + 3^2 +...+ n^2) + (1 + 2 + 3 + ...+ n)
ta có các công thức:
1^2 + 2^2 + 3^2 +...+ n^2 = n(n+1)(2n+1)/6
1 + 2 + 3 + ...+ n = n(n+1)/2
thay vào ta có:
S = n(n+1)(2n+1)/6 + n(n+1)/2
=n(n+1)/2[(2n+1)/3 + 1]
=n(n+1)(n+2)/3
4 tháng 3 2022
Bài 2:
a: Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AB=AC
AM chung
Do đó: ΔAMB=ΔAMC
Suy ra: MB=MC
b: Xét ΔADM vuông tại D và ΔAEM vuông tại E có
AM chung
\(\widehat{DAM}=\widehat{EAM}\)
Do đó:ΔADM=ΔAEM
Suy ra: MD=ME
hay ΔMDE cân tại M
c: Ta có: ΔADM=ΔAEM
nên AD=AE
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
M
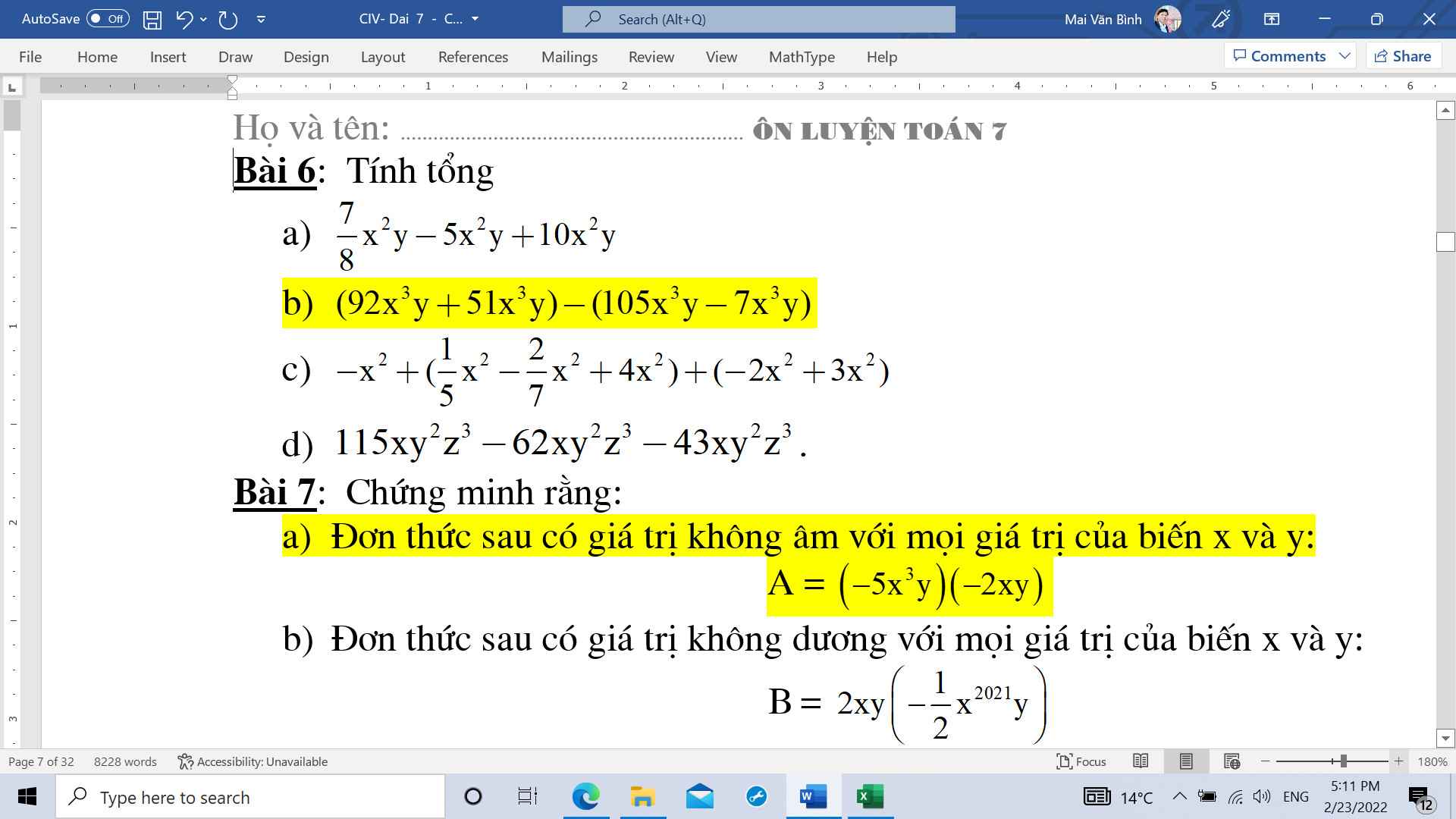
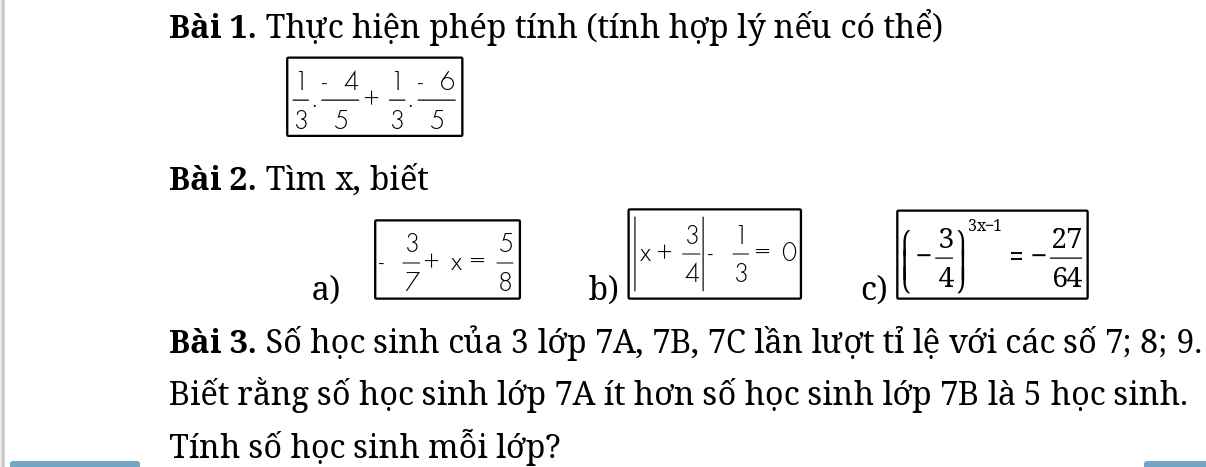Mọi người ơi , mọi người giúp mình với , mình trân thành cảm ơn
0
4)
a/ A(x)= -45-x3+4x2+ 5x+9+4x5-6x2-2
A(x)= -x3-2x2+5x+7
b/ B(x)= -3x4-2x3 +10x2 -8x+5x3-7-2x3+8x
B(x)= -3x4 +x3+10x2 -7
A(x)= -x3-2x2+5x+7
B(x)= -3x4 +x3+10x2 -7
b) P(x) = A(x)+B(x)= -x3-2x2+5x+7-3x4 +x3+10x2 -7= -3x4 +8x2+5x
Q(x)= -x3-2x2+5x+7- (-3x4 +x3+10x2 -7)= -x3-2x2+5x+7 + 3x4-x3 - 10x2 + 7= -2x3-12x2+5x+ 14