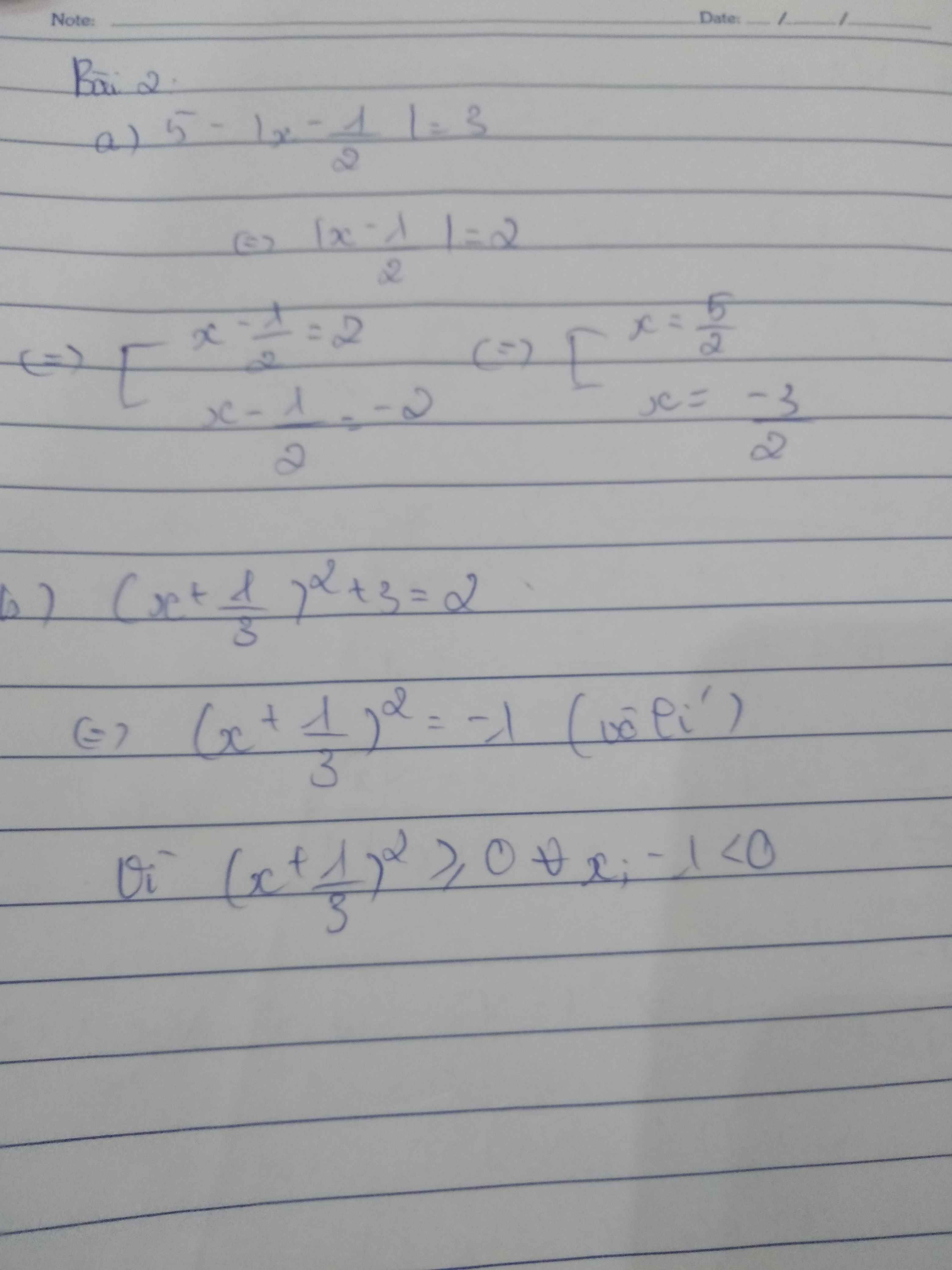K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 3 2022
Bài 2:
a: Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AB=AC
AM chung
Do đó: ΔAMB=ΔAMC
Suy ra: MB=MC
b: Xét ΔADM vuông tại D và ΔAEM vuông tại E có
AM chung
\(\widehat{DAM}=\widehat{EAM}\)
Do đó:ΔADM=ΔAEM
Suy ra: MD=ME
hay ΔMDE cân tại M
c: Ta có: ΔADM=ΔAEM
nên AD=AE
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
12 tháng 12 2018
Gọi số hoa của 3 bạn lần lượt là x, y , z
Vì x,y,z TLT vớ 4,5,6
=> x/4=y/5=z/6=k
Theo t/c dãy tỉ số bằng nhau :
k= x+y+z/ 4+5+6 = 75/15=5
=> x= 5.4=20
y= 5. 5 = 25
z= 5.6=30
Vậy ..
BN
12 tháng 12 2018
Gọi số hoa 3 bạn hái được lần lượt là a,b,c \(\left(a,b,c\inℕ^∗\right)\)
Theo đề bài ra,ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ,ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{a+b+c}{4+5+6}=\frac{75}{15}=6\)
\(\Rightarrow\hept{\begin{cases}a=6.4=24\\b=6.5=30\\c=6.6=36\end{cases}}\)
Vậy ....
12 tháng 7 2021
4)
a/ A(x)= -45-x3+4x2+ 5x+9+4x5-6x2-2
A(x)= -x3-2x2+5x+7
b/ B(x)= -3x4-2x3 +10x2 -8x+5x3-7-2x3+8x
B(x)= -3x4 +x3+10x2 -7
12 tháng 7 2021
A(x)= -x3-2x2+5x+7
B(x)= -3x4 +x3+10x2 -7
b) P(x) = A(x)+B(x)= -x3-2x2+5x+7-3x4 +x3+10x2 -7= -3x4 +8x2+5x
Q(x)= -x3-2x2+5x+7- (-3x4 +x3+10x2 -7)= -x3-2x2+5x+7 + 3x4-x3 - 10x2 + 7= -2x3-12x2+5x+ 14
14 tháng 7 2021
Vì BC và Cx là 2 tia đối nên \(\widehat{BCA}\) và \(\widehat{ACx}\) là 2 góc kề bù
\(\Rightarrow\widehat{ACB}+\widehat{ACx}=180^o\)
\(40^o+\widehat{ACx}=180^o\)
\(\widehat{ACx}=140^o\)
b) Ta có:\(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\) (tổng 3 góc trong 1 tam giác)
\(40^o+\widehat{ABC}+70^o=180^o\)
\(\widehat{ABC}=70^o\)(1)
Vì Oy là phân giác của \(\widehat{ACx}\) nên \(\widehat{xCy}=\dfrac{\widehat{ACx}}{2}=\dfrac{140^o}{2}=70^o\)(2)
Từ (1),(2) => \(\widehat{ABC}=\widehat{xCy}\)
c)Cặp góc đồng vị là \(\widehat{ABC}\) và \(\widehat{xCy}\)
1 tháng 2 2022
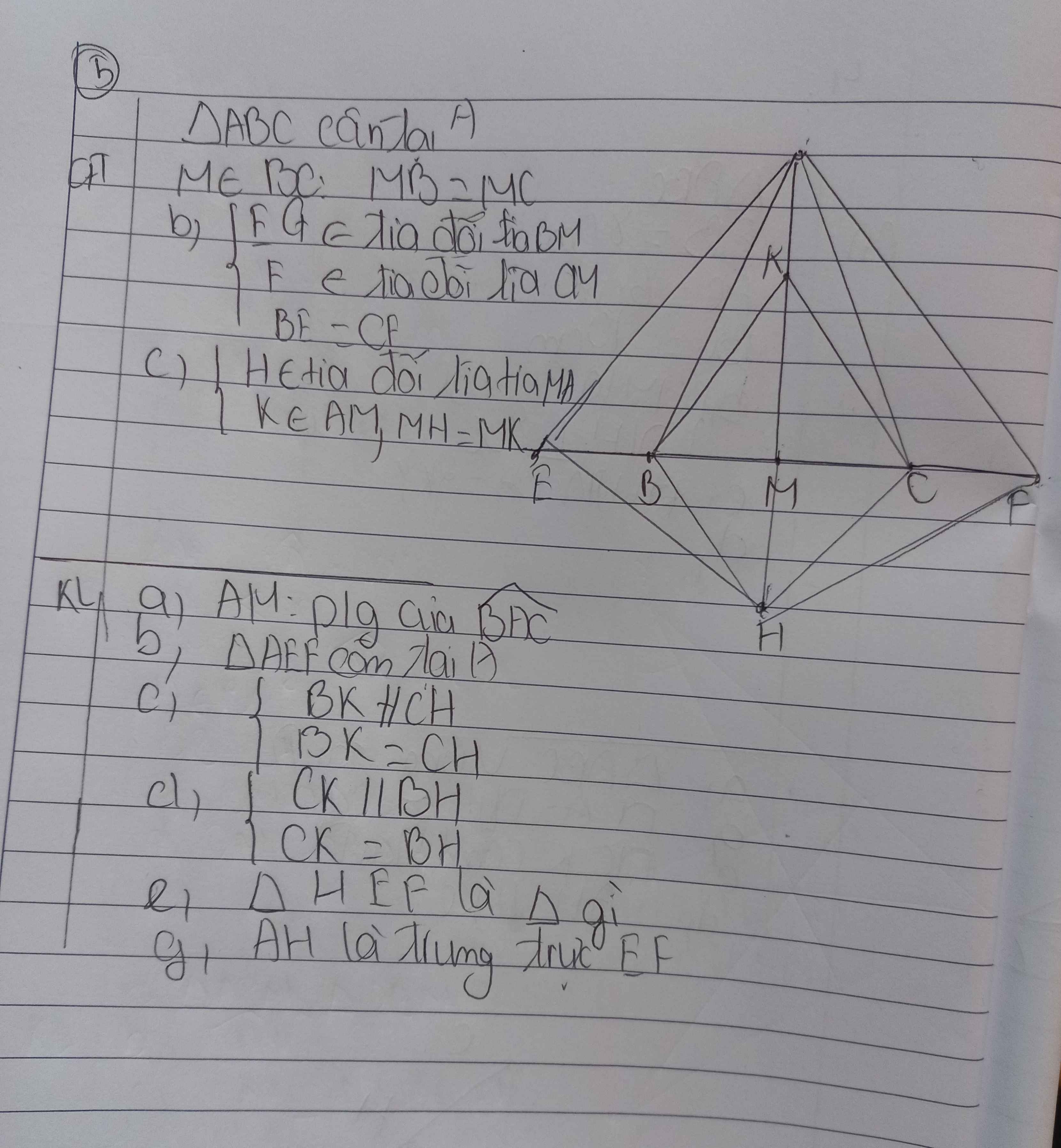
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Xét ΔABE và ΔACF có
AB=AC
\(\widehat{ABE}=\widehat{ACF}\)
BE=CF
Do đó: ΔABE=ΔACF
c: Xét tứ giác BKCH có
M là trung điểm của BC
M là trung điểm của HK
Do đó: BKCH là hình bình hành
Suy ra: BK//CH; BK=CH
d: Ta có: BKCH là hình bình hành
nên CK//BH; CK=BH
