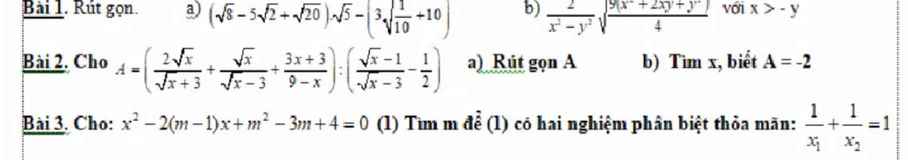K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
A
1
12 tháng 12 2021
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
NT
3
19 tháng 8 2021
\(P=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right):\frac{\sqrt{x}}{x+\sqrt{x}}\)ĐK : x > 0
\(=\left(\frac{\sqrt{x}+1+x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\frac{1}{\sqrt{x}+1}=\frac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P=\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{3}{\sqrt{x}+1}-\frac{6\sqrt{x}-4}{x-1}\)
\(=\frac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{x-1}=\frac{x-2\sqrt{x}+1}{x-1}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)
10 tháng 6 2021
1.2 với \(x\ge0,x\in Z\)
A=\(\dfrac{2\sqrt{x}+7}{\sqrt{x}+2}=2+\dfrac{3}{\sqrt{x}+2}\in Z< =>\sqrt{x}+2\inƯ\left(3\right)=\left(\pm1;\pm3\right)\)
*\(\sqrt{x}+2=1=>\sqrt{x}=-1\)(vô lí)
*\(\sqrt{x}+2=-1=>\sqrt{x}=-3\)(vô lí
*\(\sqrt{x}+2=3=>x=1\)(TM)
*\(\sqrt{x}+2=-3=\sqrt{x}=-5\)(vô lí)
vậy x=1 thì A\(\in Z\)
NA
0
12 tháng 12 2021
\(b,\Leftrightarrow\left\{{}\begin{matrix}m+2=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=-1\\ c,\text{PT giao Ox: }y=0\Leftrightarrow\left(m+2\right)x-m=0\\ \text{Thay }x=2\Leftrightarrow2m+4-m=0\\ \Leftrightarrow m=-4\\ d,\text{PT giao Ox và Oy: }\\ y=0\Leftrightarrow x=\dfrac{m}{m+2}\Leftrightarrow A\left(\dfrac{m}{m+2};0\right)\Leftrightarrow OA=\left|\dfrac{m}{m+2}\right|\\ x=0\Leftrightarrow y=-m\Leftrightarrow B\left(0;-m\right)\Leftrightarrow OB=\left|m\right|\\ \Delta OAB\text{ cân }\Leftrightarrow OA=OB\Leftrightarrow\left|\dfrac{m}{m+2}\right|=\left|m\right|\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{m}{m+2}=m\\\dfrac{m}{m+2}=-m\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\left(m+1\right)=0\\m\left(m+3\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-1\\m=-3\end{matrix}\right.\)
ND
1
T
1
PN
1
16 tháng 1 2022
Câu 3:
\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-3m+4\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-3m+4\right)\)
\(=4m^2-16m+4-4m^2+12m-16=-4m-12\)
Để phương trình có hai nghiệm phân biệt thì -4m-12>0
=>-4m>12
hay m<-3
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3m+4\end{matrix}\right.\)
Theo đề, ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow m^2-3m+4-2m+2=0\)
=>(m-2)(m-3)=0
hay \(m\in\varnothing\)
