K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
17 tháng 9 2021
1.1.
\(sinx=\dfrac{1}{4}\Leftrightarrow\left[{}\begin{matrix}x=arcsin\dfrac{1}{4}+k2\pi\\x=\pi-arcsin\dfrac{1}{4}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 9 2021
Bài 1:
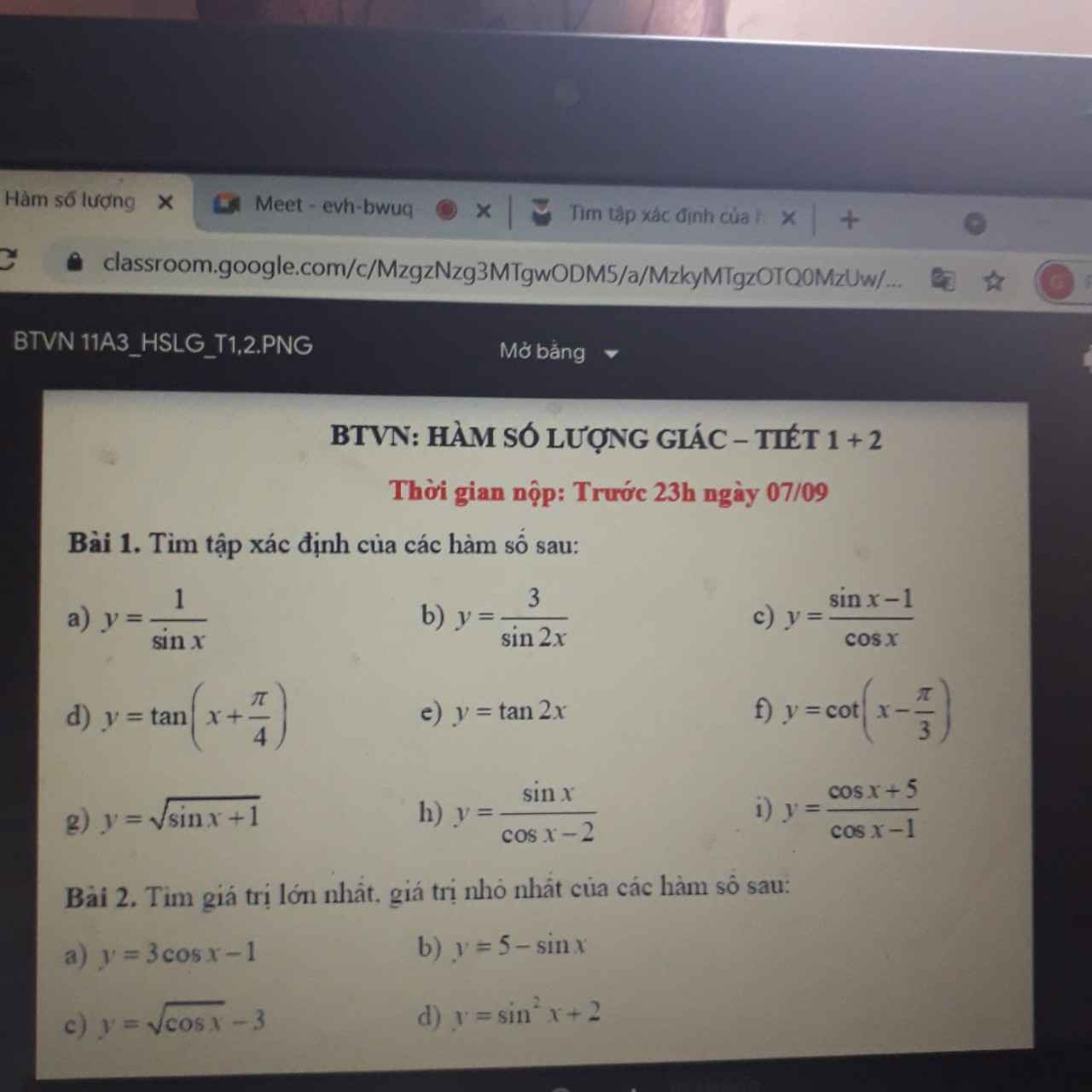
ĐKXĐ:
a. \(sinx\ne0\Rightarrow x\ne k\pi\)
b. \(sin2x\ne0\Rightarrow2x\ne k\pi\Rightarrow x\ne\dfrac{k\pi}{2}\)
c. \(cosx\ne0\Rightarrow x\ne\dfrac{\pi}{2}+k\pi\)
d. \(cos\left(x+\dfrac{\pi}{4}\right)\ne0\Rightarrow x+\dfrac{\pi}{4}\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{4}+k\pi\)
e. \(cos2x\ne0\Rightarrow2x\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
f. \(sin\left(x-\dfrac{\pi}{3}\right)\ne0\Rightarrow x-\dfrac{\pi}{3}\ne k\pi\Rightarrow x\ne\dfrac{\pi}{3}+k\pi\)
g. \(sinx+1\ge0\Rightarrow D=R\)
h. \(cosx-2\ne0\Rightarrow D=R\)
i. \(cosx-1\ne0\Rightarrow cosx\ne1\Rightarrow x\ne k2\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 9 2021
Bài 2:
a.
\(-1\le cosx\le1\Rightarrow-3\le3cosx\le3\Rightarrow-4\le y\le2\)
\(y_{min}=-4\) khi \(cosx=-1\)
\(y_{max}=2\) khi \(cosx=1\)
b.
\(-1\le sinx\le1\Rightarrow-1\le-sinx\le1\) \(\Rightarrow4\le y\le6\)
\(y_{min}=4\) khi \(sinx=1\)
\(y_{max}=6\) khi \(cosx=1\)
c.
\(0\le\sqrt{cosx}\le1\Rightarrow-3\le y\le-2\)
\(y_{min}=-3\) khi \(cosx=0\)
\(y_{max}=-2\) khi \(cosx=1\)
d.
\(0\le sin^2x\le1\Rightarrow2\le y\le3\)
\(y_{min}=2\) khi \(sinx=0\)
\(y_{max}=3\) khi \(sin^2x=1\Leftrightarrow cosx=0\)
AH
Akai Haruma
Giáo viên
31 tháng 7 2021
Lời giải:
Gọi $C'(a,b)$ là ảnh của $C$ đối xứng qua $x=1$
$\overrightarrow{CC'}=(a+5,b+1)\perp \overrightarrow{u_d}(1,0)$
$\Rightarrow a+5+0(b+1)=0$
$\Leftrightarrow a=-5$
$C$ đối xứng với $C'$ qua $d$ thì $CC'$ cắt $d$ tại trung điểm của nó
$\Rightarrow \frac{b-1}{2}=1$
$\Leftrightarrow b=3$
Vậy $M'(-5,3)$
MT
2
26 tháng 8 2021
Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
\(y'=\left(m-1\right)x^2+2mx+3m-2\)
Với \(m=1\) ko thỏa mãn
\(y'>0\) ; \(\forall x\in R\) khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1>0\\\Delta'=m^2-\left(3m-2\right)\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\2m^2-5m+2>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left[{}\begin{matrix}m>2\\m< \dfrac{1}{2}\\\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow m>2\)
DL
0
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2021
Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)
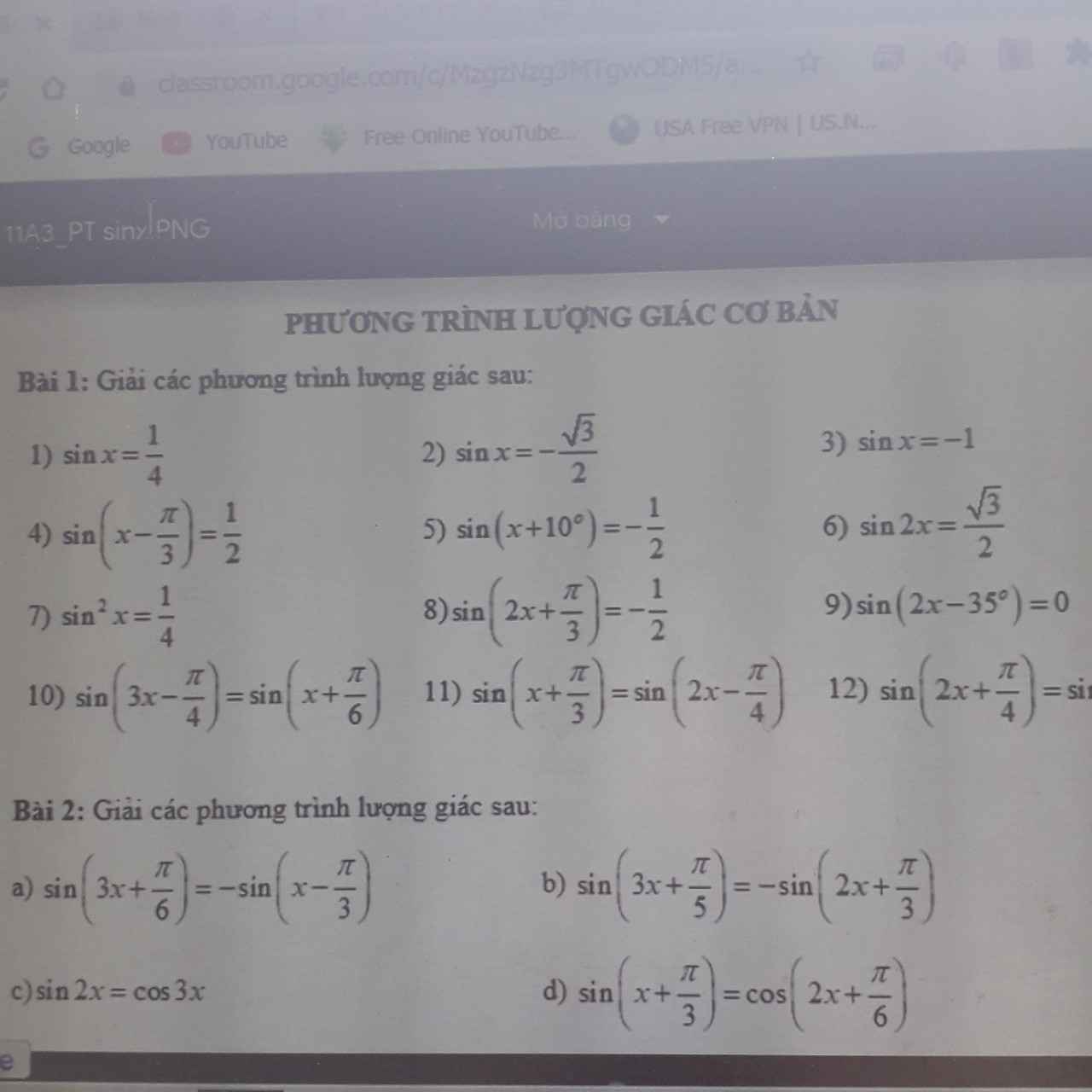
Quy tắc b và c là phép biến hình (quy tắc b là phép đối xứng trục, quy tắc c là phép đối xứng tâm)