BL
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
2
26 tháng 8 2021
a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD
b: Ta có: ΔABD=ΔHBD
nên \(\widehat{BAD}=\widehat{BHD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BHD}=90^0\)
hay DH\(\perp\)BC
LT
1
30 tháng 8 2021
Bài 2:
a: Ta có: Om là tia phân giác của \(\widehat{xOy}\)
nên \(\widehat{xOm}=\widehat{yOm}=\dfrac{180^0}{2}=90^0\)
Do đó: Om\(\perp\)xy
b: Ta có: \(\widehat{xOa}+\widehat{mOa}=90^0\)
\(\widehat{mOb}+\widehat{yOb}=90^0\)
mà \(\widehat{mOa}=\widehat{yOb}\)
nên \(\widehat{xOa}=\widehat{mOb}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 12 2022
Mình không nhìn thấy câu hỏi, giờ mới thấy bạn ạ
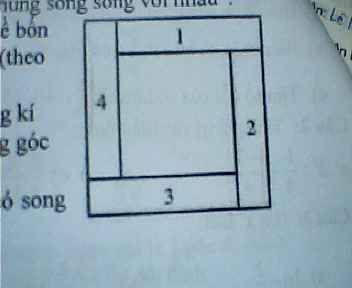
Do mở rộng cạnh của thửa đất về cả bốn phía nên thửa đất mới sau khi mở rộng cũng là hình vuông. mỗi cạnh của thửa đất lúc sau đã tăng :
0,5 x 2 = 1 (m)
Gọi cạnh hình vuông lúc đầu là x đk x > 0
Thì cạnh hình vuông lúc sau là : x + 1
theo bài ra ta có : (x + 1)( x + 1) - x2 = 20
x2 + x + x + 1 - x2 = 20
2x = 20 -1
2x = 19
x = 19: 2
x = 9,5
Kết luận cạnh hình vuông lúc đầu là 9,5 m
DT
3
17 tháng 8 2019
Ta có: \(14x=21y=16z\)=> \(\frac{x}{\frac{1}{14}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\) => \(\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}=\frac{2x+y-z}{\frac{1}{7}+\frac{1}{21}-\frac{1}{16}}=\frac{2}{\frac{43}{336}}=\frac{672}{43}\)
=> \(\hept{\begin{cases}\frac{x}{\frac{1}{14}}=\frac{672}{43}\\\frac{y}{\frac{1}{21}}=\frac{672}{43}\\\frac{z}{\frac{1}{16}}=\frac{672}{43}\end{cases}}\) => \(\hept{\begin{cases}x=\frac{672}{43}.\frac{1}{14}=\frac{48}{43}\\y=\frac{672}{43}.\frac{1}{21}=\frac{32}{43}\\z=\frac{672}{43}.\frac{1}{16}=\frac{42}{43}\end{cases}}\)
Vậy ...
17 tháng 8 2019
\(\Rightarrow\frac{x}{\frac{1}{14}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\)
\(\Rightarrow\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\)
+ Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}=\frac{2x+y-z}{\frac{1}{7}+\frac{1}{21}-\frac{1}{16}}=\frac{2}{\frac{43}{336}}=\frac{672}{43}\)
Suy ra \(\frac{2x}{\frac{1}{7}}=\frac{672}{43}\Rightarrow x=\frac{48}{43}\)
\(\frac{y}{\frac{1}{21}}=\frac{672}{43}\Rightarrow y=\frac{32}{43}\)
\(\frac{z}{\frac{1}{16}}=\frac{672}{43}\Rightarrow z=\frac{42}{43}\)
Vậy \(x=\frac{48}{43};y=\frac{32}{43};z=\frac{42}{43}\)
Chúc bạn học tốt !!!
AH
Akai Haruma
Giáo viên
19 tháng 8 2021
Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x+2020|+|x+2021|=|x+2020|+|-(x+2021)|$
$\geq |x+2020-(x+2021)|=1$
Vậy GTNN của biểu thức là $1$. Giá trị này đạt tại $(x+2020).-(x+2021)\geq 0$
$(x+2020)(x+2021)\leq 0$
$-2021\leq x\leq -2020$
HN
1
26 tháng 8 2021
a: Xét ΔIMC vuông tại I và ΔINC vuông tại I có
IM=IN
CI chung
Do đó: ΔIMC=ΔINC
b: Xét ΔCKB có
M là trung điểm của BC
MN//KB
Do đó: N là trung điểm của CK
20 tháng 4 2016
Gia sử AC > AB
Trên tia AC lấy M sao cho AB=AM
AD là tia phân giác góc A=>góc CAD=góc BAD
Tam giác AME và tam giác ABE có:
Góc CAD=góc BAD
MA=AB
AE:cạnh chung
=>tam giác AME = Tam giác ABE
=>ME=BE(Cạnh tương ứng)
Ta có:M thuộc AC =>AM+MC=AC
=>AC-AB=(AM+MC)-AB
Mà AM=MB=>(AM+MC)-AB=MC
Tam giác CEM có:MC>CE-ME(Bất đẳng thức tam giác)
Mà ME=BE=>MC>CE-BE
hay AC-AB>EC-EB
