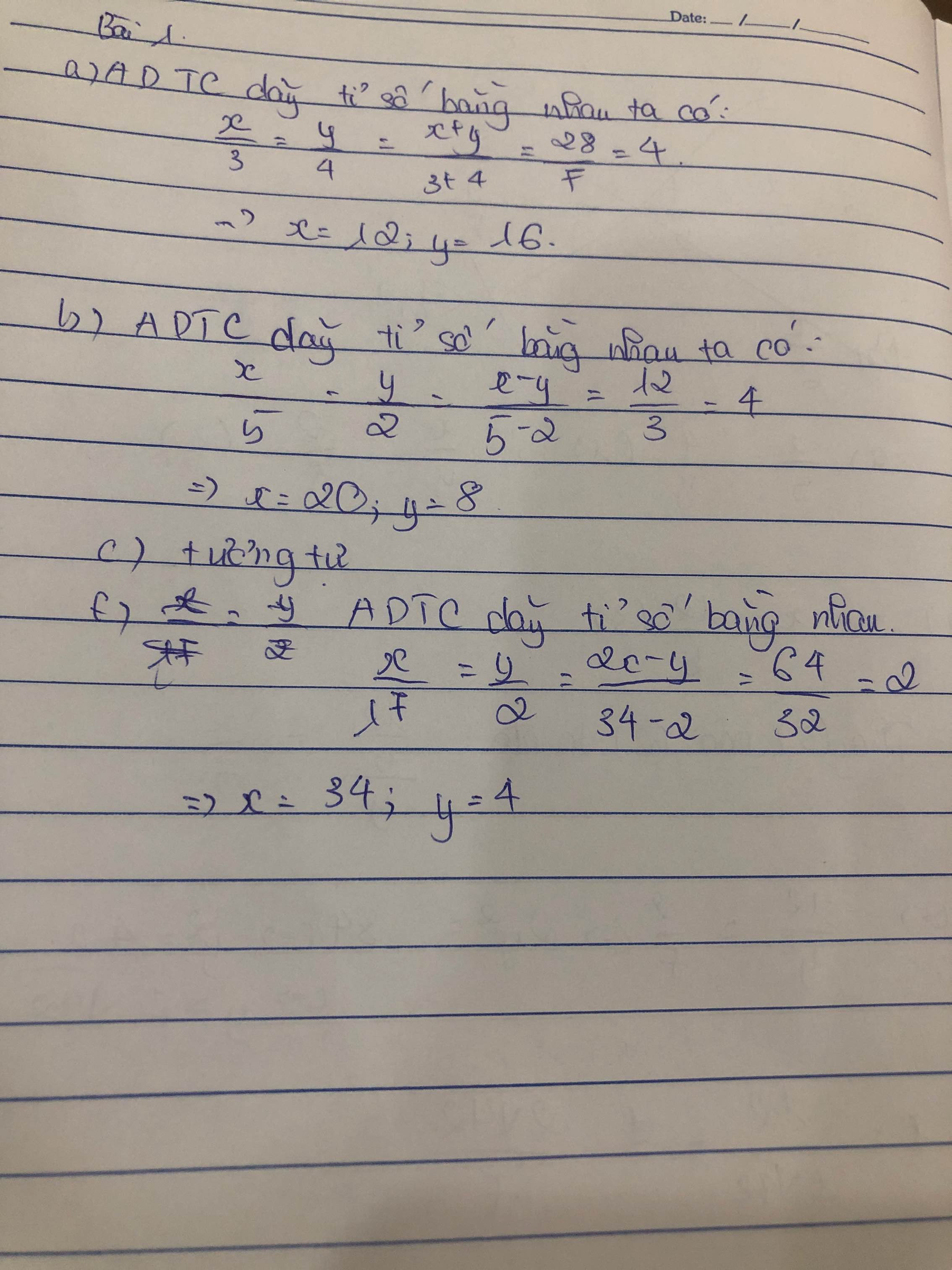Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{7}=\dfrac{b}{8}=\dfrac{c}{9}=\dfrac{a+b+c}{7+8+9}=\dfrac{120}{24}=5\)
Do đó: a=35; b=40; c=45

Bài 5:
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y-z}{2+3-4}=\dfrac{-20}{1}=-20\)
Do đó: x=-40; y=-60; z=-80

\(2,\\ a,=7^{5+8}=7^{13}\\ b,=5^{8-5}=5^3\\ c,=\dfrac{1}{3^2}=\dfrac{1}{9}\\ d,=\dfrac{2^9}{2^{10}}=\dfrac{1}{2}\\ e,=\dfrac{3^9}{3^{12}}=\dfrac{1}{3^3}=\dfrac{1}{27}\\ f,=\dfrac{5^6}{5^3}=5^3=125\\ g,=\dfrac{\left(2\cdot3\right)^{12}\cdot2^2}{6^{11}}=\dfrac{6^{12}\cdot2^2}{6^{11}}=6\cdot4=24\\ h,=\dfrac{2^{18}\cdot3^{18}}{3^{18}\cdot2^{15}}=2^3=8\)

\(\left(\frac{4}{5}x^4y^2\right)\left(\frac{5}{9}xy\right)=\left(\frac{4}{5}\cdot\frac{5}{9}\right)\left(x^4x\right)\left(y^2y\right)=\frac{4}{9}x^5y^3\)

a: XétΔCHA vuông tại H và ΔCHD vuông tại H có
CH chung
HA=HD
=>ΔCHA=ΔCHD
=>CA=CD
b: DM vuông góc AC
AB vuông góc AC
=>DM//AB
=>góc HDK=góc HAB
Xét ΔHAB vuông tại H và ΔHDK vuông tại H có
HA=HD
góc HAB=góc HDK
=>ΔHAB=ΔHDK
=>HB=HK
=>H là trung điểm của BK
d: Xét ΔCAD có
AF.CH,MD là đường cao
=>AF,CH,MD đồng quy
=>A,K,F thẳng hàng

a) dấu hiệu ở đây là tuổi nghề một số công nhân trong một phân xưởng
số giá trị là 30
b)
Số giá trị (x) 3 4 5 6 7 8 9 10 15
tần số (n) 1 2 3 2 6 7 1 10 2
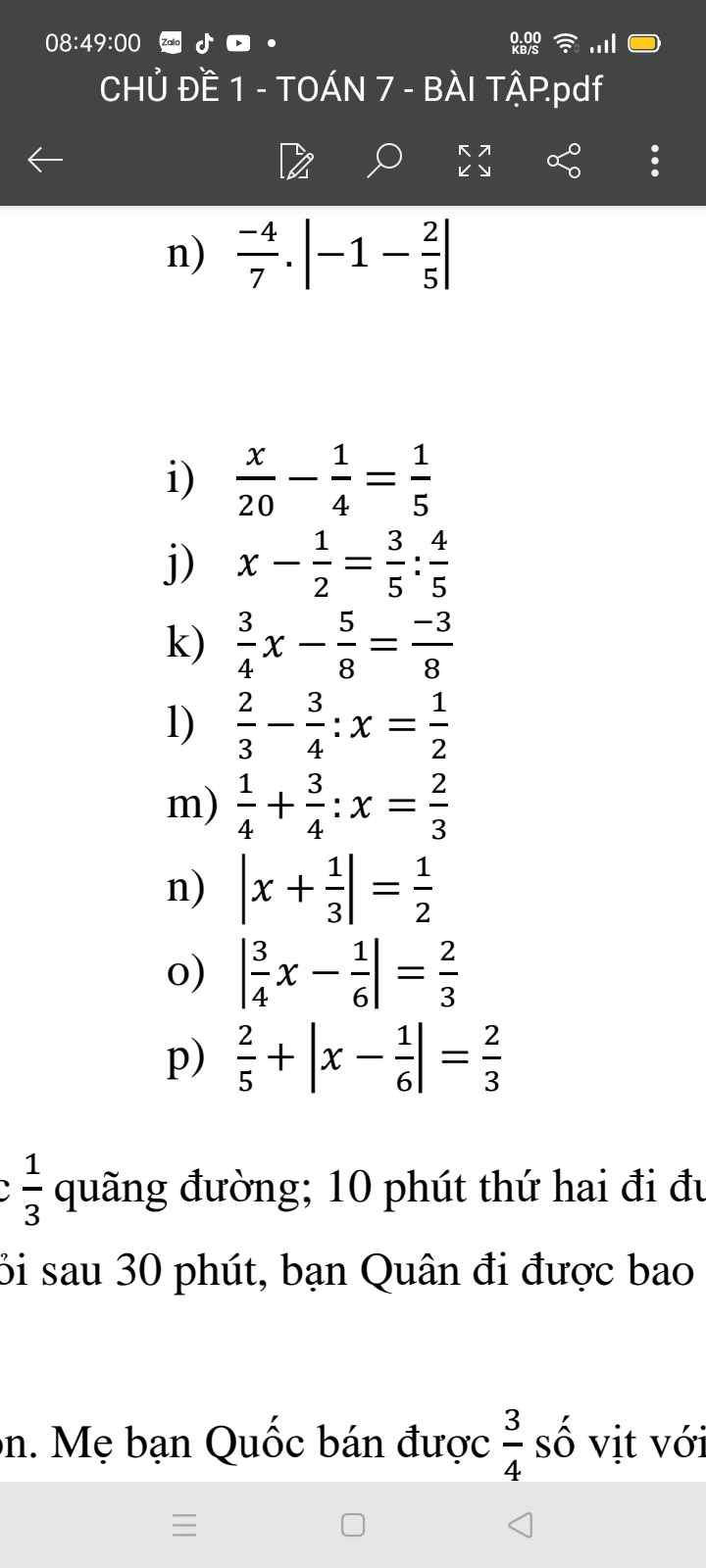
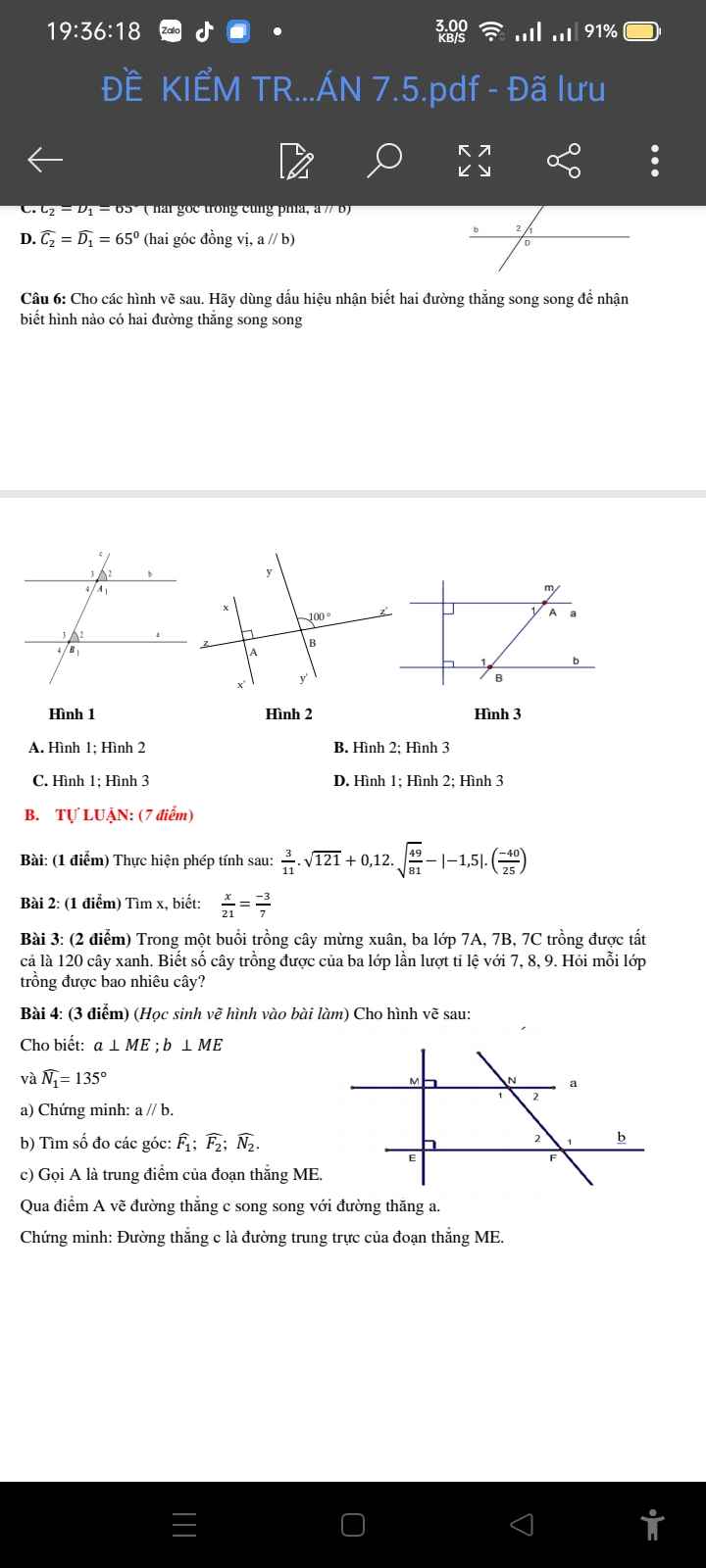
 mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33