
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(\widehat{BAC}+\widehat{xAC}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{xAC}=100^0\)
\(\Leftrightarrow\widehat{xAt}=\widehat{CAt}=\dfrac{\widehat{xAC}}{2}=\dfrac{100^0}{2}=50^0\)
b) Ta có: \(\widehat{CAt}=\widehat{BCA}\left(=50^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên At//BC(Dấu hiệu nhận biết hai đường thẳng song song)

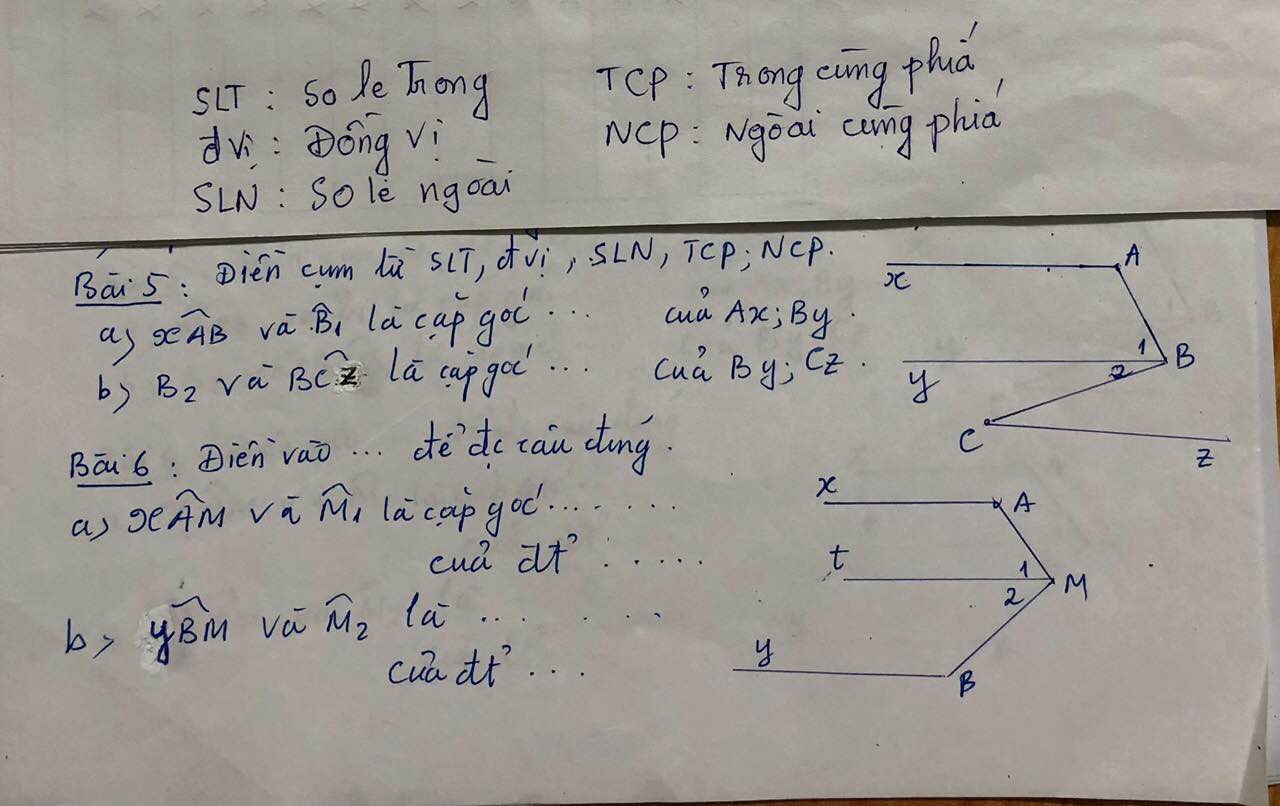
6.
a.trong cùng phía/Ax và Mt
b.trong cùng phía/By và Mt
( Nó khác gì bài 5 đâu nhỉ?)

\(B=\frac{2x-1}{x+5}\)
\(\Rightarrow B=\frac{2x+10-11}{x+5}\)
\(\Rightarrow B=2-\frac{11}{x+5}\)
Để \(B\in Z\)
\(\Rightarrow x+5\in\left(1;11;-1;-11\right)\)
\(\Rightarrow x\in\left(-4;6;-6;-16\right)\)
\(B=\frac{2x-1}{x+5}=\frac{2\left(x+5\right)-9}{x+5}=\frac{2\left(x+5\right)}{x+5}-\frac{9}{x+5}=2-\frac{9}{x+5}\)
Rút gọn biểu thức B ta được \(B=2-\frac{9}{x+5}\)hoặc \(B=\frac{2x}{x+5}-\frac{1}{x+5}\)
ĐKXĐ của B : \(x+5\ne0\Rightarrow x\ne-5\)
P/S : Đề ko có yêu cầu gì hết nên mình chỉ làm vậy thôi

Vì BC và Cx là 2 tia đối nên \(\widehat{BCA}\) và \(\widehat{ACx}\) là 2 góc kề bù
\(\Rightarrow\widehat{ACB}+\widehat{ACx}=180^o\)
\(40^o+\widehat{ACx}=180^o\)
\(\widehat{ACx}=140^o\)
b) Ta có:\(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\) (tổng 3 góc trong 1 tam giác)
\(40^o+\widehat{ABC}+70^o=180^o\)
\(\widehat{ABC}=70^o\)(1)
Vì Oy là phân giác của \(\widehat{ACx}\) nên \(\widehat{xCy}=\dfrac{\widehat{ACx}}{2}=\dfrac{140^o}{2}=70^o\)(2)
Từ (1),(2) => \(\widehat{ABC}=\widehat{xCy}\)
c)Cặp góc đồng vị là \(\widehat{ABC}\) và \(\widehat{xCy}\)










1) Vì a⊥d , b⊥d ⇒ a // b
⇒\(\widehat{A_1}=\widehat{B}=80^o\) (ở vị trí so le trong)
⇒\(\widehat{A_3}=\widehat{B}=80^o\)(ở vị trí đồng vị)
Do \(\widehat{A_2}+\widehat{B}=180^o\)
(hai góc trong cùng phía)
Thay số:\(\widehat{A_2}+80^o=180^o\)
⇒\(\widehat{A_2}=100^o\)
2)a.Vì Ax//By⇒\(\widehat{A}=\widehat{ABy}=30^o\)
Mà \(\widehat{ABC}=70^o\)
\(\Rightarrow\widehat{yBC}=\widehat{ABC}-\widehat{CBy}=70^o-30^o=40^o\)
b. Xét Bx và Ct có :\(\widehat{CBy}=\widehat{C}=40^o\) là hai góc so le trong bằng nhau
⇒Bx//Ct . Mà Ax//By
⇒Ax//Ct