
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 5:
\(\Leftrightarrow-x^2+7x-9+2x-9=0\)
\(\Leftrightarrow x^2-9x+18=0\)
=>x=3
=>Chọn A


ĐKXĐ: \(1\le x\le4\)
Đặt \(\sqrt{x-1}+\sqrt{4-x}=t\Rightarrow t^2=3+2\sqrt{\left(x-1\right)\left(4-x\right)}\)
\(\Rightarrow-\sqrt{\left(x-1\right)\left(4-x\right)}=-\dfrac{1}{2}t^2+\dfrac{3}{2}\)
Ta có:
\(\sqrt{x-1}+\sqrt{4-x}\le\sqrt{2\left(x-1+4-x\right)}=\sqrt{6}\)
\(\sqrt{x-1}+\sqrt{4-x}\ge\sqrt{x-1+4-x}=\sqrt{3}\)
\(\Rightarrow t\in\left[\sqrt{3};\sqrt{6}\right]\)
Phương trình trở thành:
\(-\dfrac{1}{2}t^2+t+\dfrac{3}{2}=m\)
Xét hàm \(f\left(t\right)=-\dfrac{1}{2}t^2+t+\dfrac{3}{2}\) với \(t\in\left[\sqrt{3};\sqrt{6}\right]\)
\(a=-\dfrac{1}{2}< 0;-\dfrac{b}{2a}=1< \sqrt{3}\)
\(\Rightarrow f\left(t\right)\) nghịch biến trên \(\left[\sqrt{3};\sqrt{6}\right]\)
\(\Rightarrow f\left(\sqrt{6}\right)\le f\left(t\right)\le f\left(\sqrt{3}\right)\Rightarrow\dfrac{-3+2\sqrt{6}}{2}\le f\left(t\right)\le\sqrt{3}\)
Vậy pt đã cho có nghiệm khi \(\dfrac{-3+2\sqrt{6}}{2}\le m\le\sqrt{3}\)



Tờ 1
Câu 1: A
Câu 2: B
Câu 3: C
Câu 4: B
Câu 1 dạng 2: D
Tờ 2:
Câu 2: 14 không phải số nguyên tố
Câu 3: D
Câu 1: A
Câu 2: B
Câu 3: B
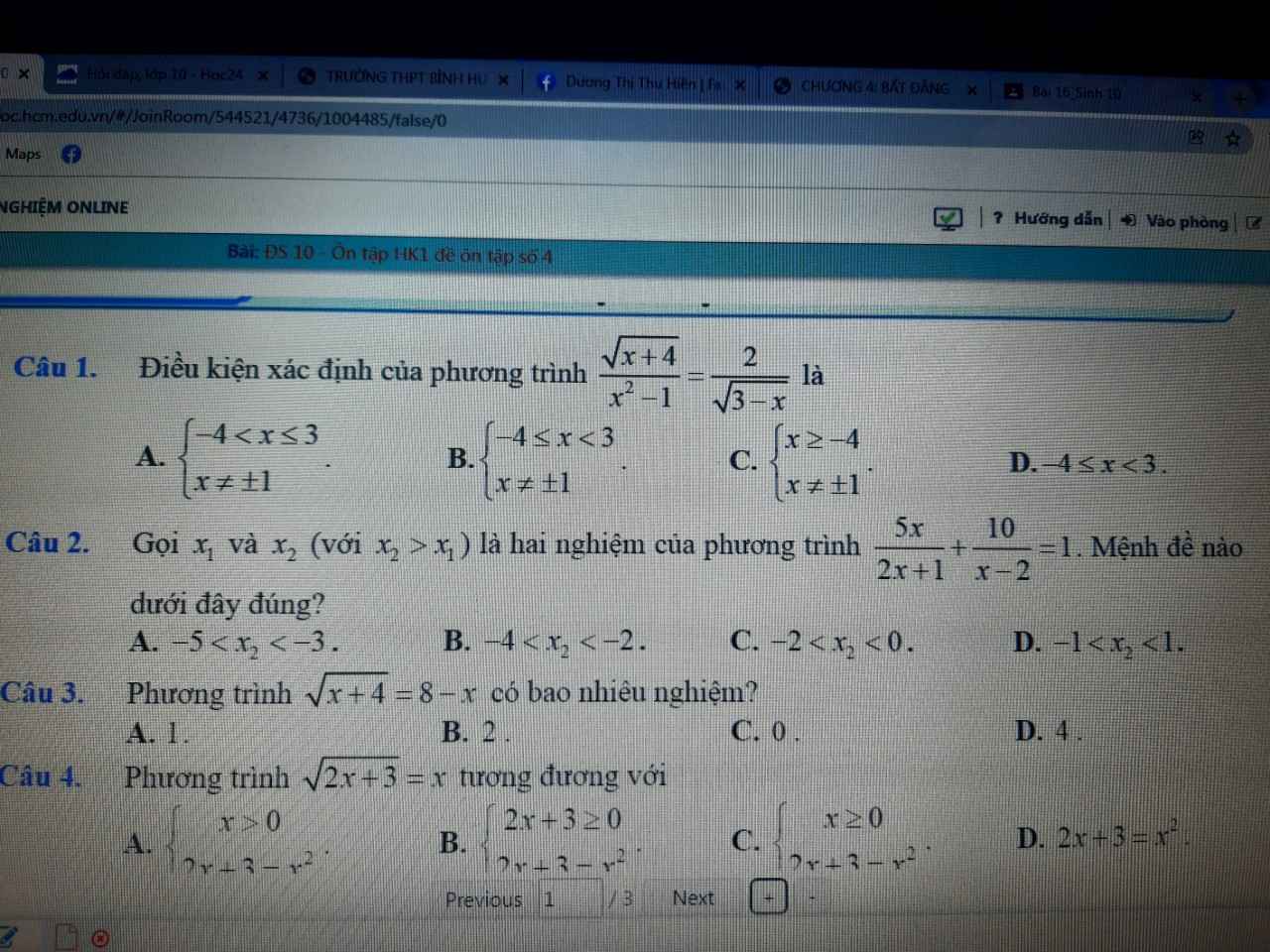
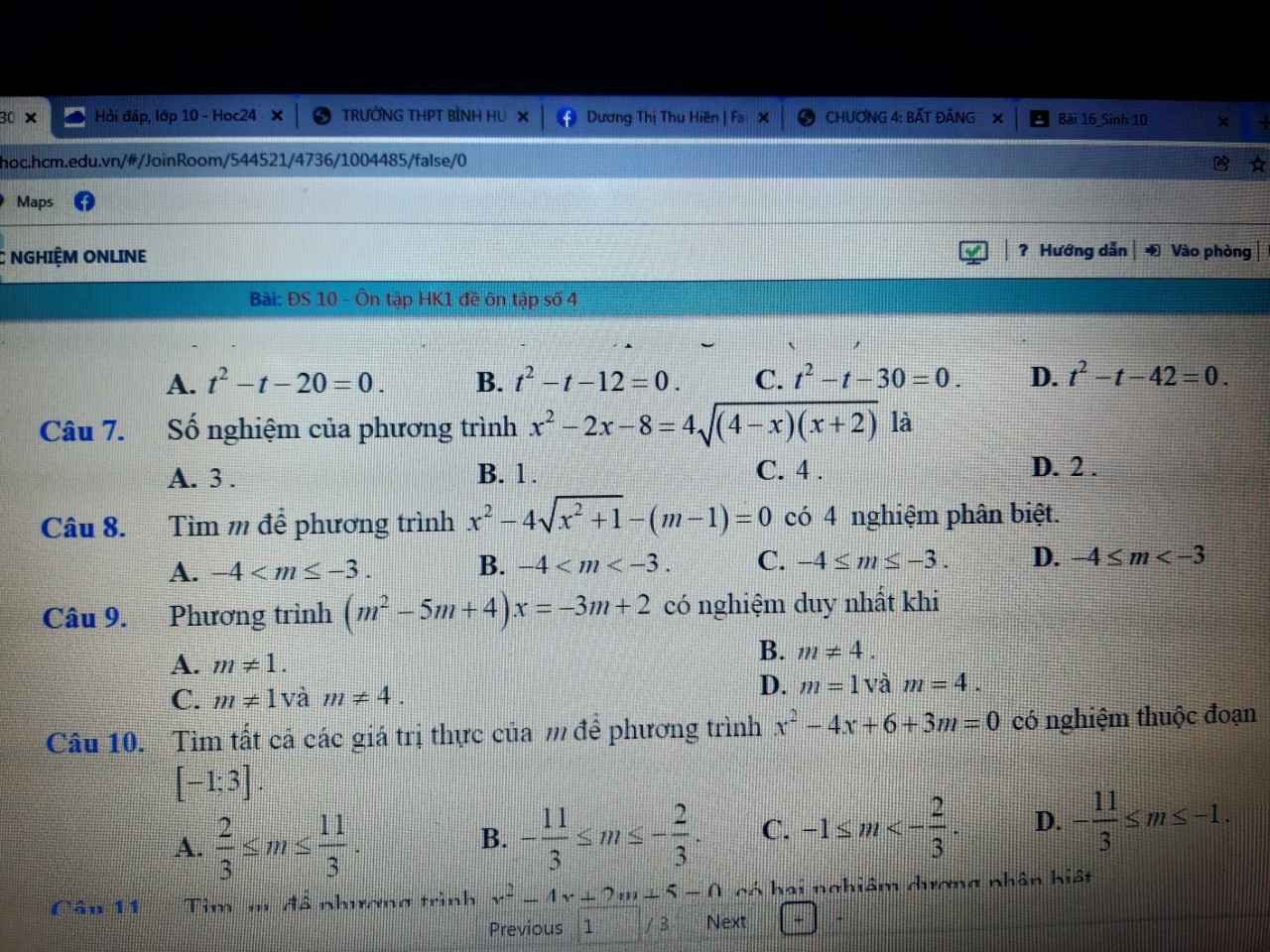

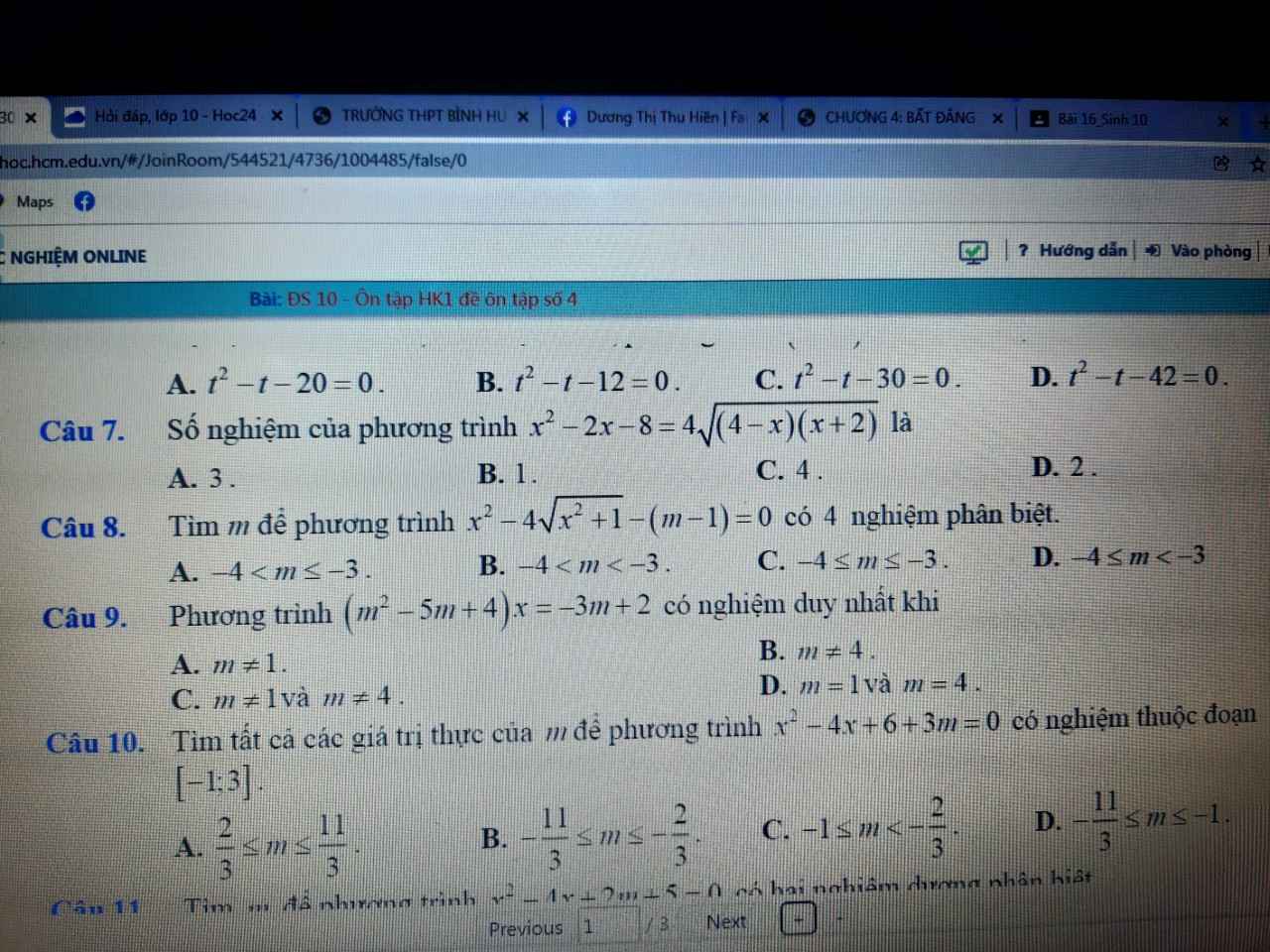
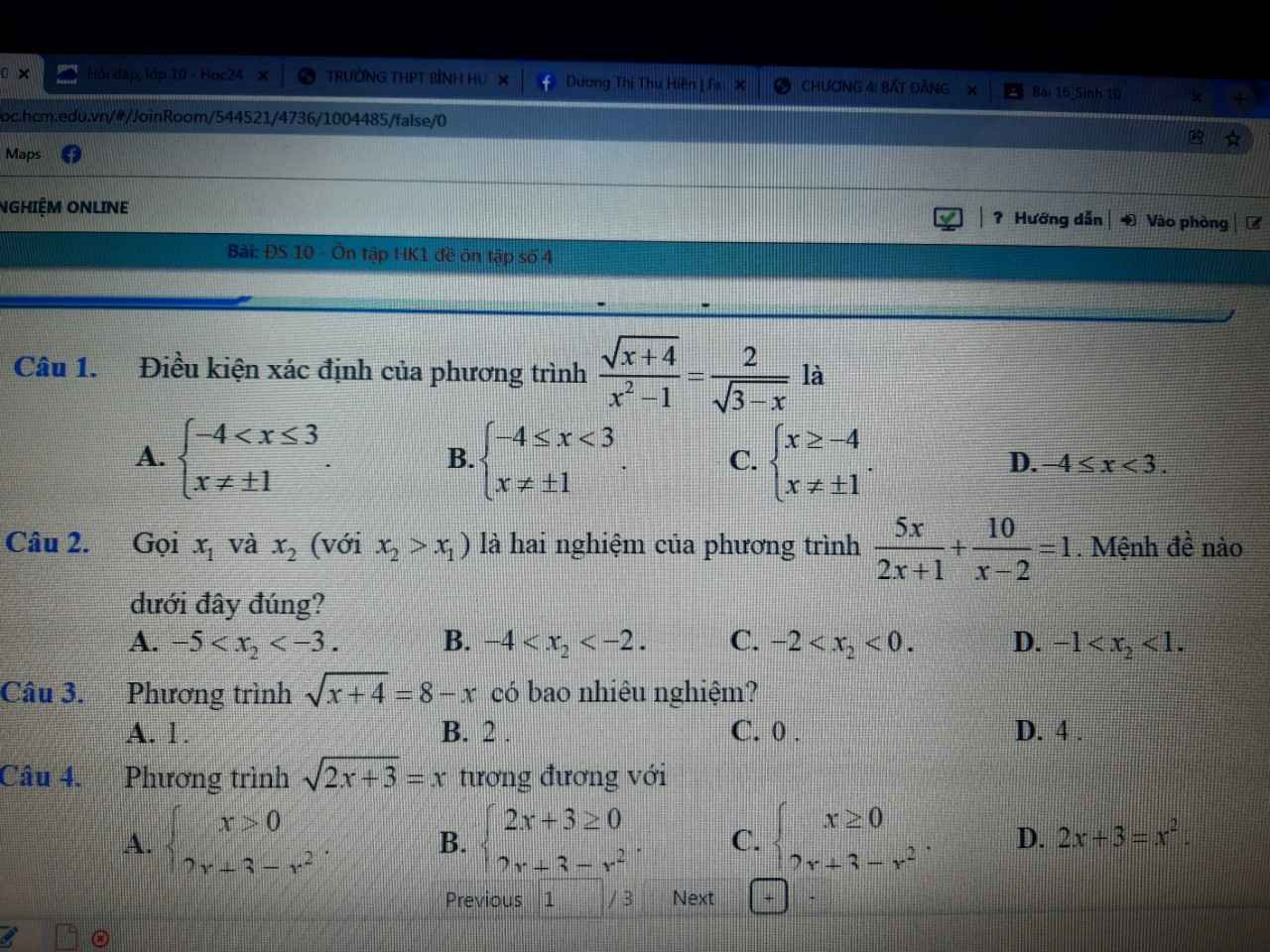
 làm giúp e câu này với ạ
làm giúp e câu này với ạ






Câu 2: B
Câu 9: C